Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
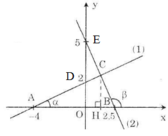
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
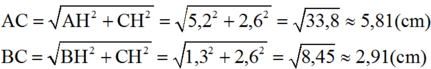
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
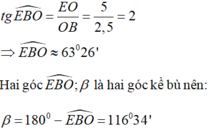
Phương trình hoành độ giao điểm của d 1 v à d 2 là:
4 − x 3 = 8 − 2 x ⇔ 24 – 6 x = 4 – x ⇔ 5 x = 20 ⇒ x = 4 ⇒ y = 0 nên A (4; 0)
+) B (0; yB) là giao điểm của đường thẳng d1 và trục tung. Khi đó y B = 4 − 0 3
y B = 4 3
Suy ra tổng tung độ y A + y B = 0 + 4 3 = 4 3
Đáp án cần chọn là: A
\(a,PTHDGD:2x-1=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow M\left(1;1\right)\\ b,\text{Gọi đt của }\left(d\right)\text{ là }y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x+4\)
a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)
b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)
Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
và y = – x + 2 
qua gốc tọa độ và song song với 
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x+3=0,5x-2\\y=-2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}x=0\\y=-2\cdot0+3=3\end{matrix}\right.\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x=0\\y=0.5\cdot0-2=-2\end{matrix}\right.\)
Vậy: A(0;3); B(0;-2); C(2;-1)
\(AB=\sqrt{\left(0-0\right)^2+\left(-2-3\right)^2}=5\)
\(AC=\sqrt{\left(2-0\right)^2+\left(-1-3\right)^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(2-0\right)^2+\left(-1+2\right)^2}=\sqrt{5}\)
Vì \(AC^2+BC^2=AB^2\) nên ΔABC vuông tại C
\(S_{BAC}=\dfrac{AC\cdot BC}{2}=\dfrac{2\sqrt{5}\cdot\sqrt{5}}{2}=5\left(đvdt\right)\)
a. -2x+3=0,5x-2
2,5x = 5
=> x= 2
=> y = -1
Vậy C ( 2;-1 ) là giao điểm của (di ) (dz )