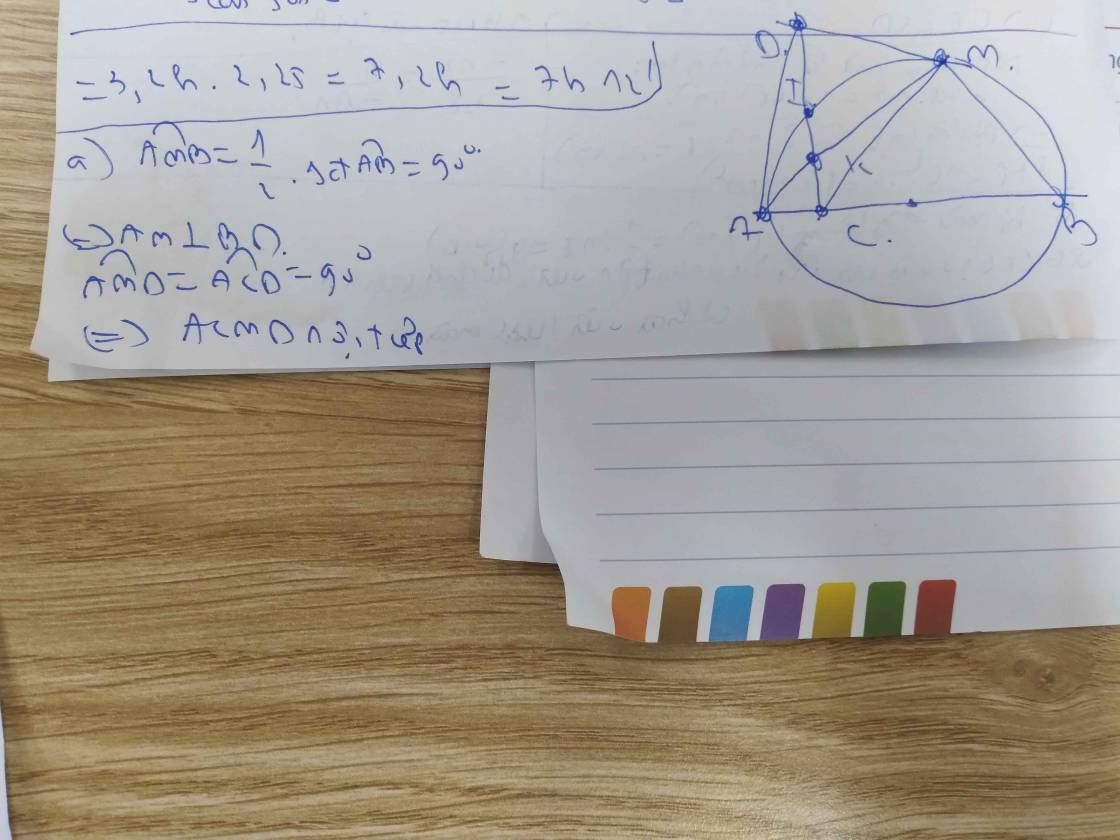
GIÚP EM VỚI ẠCho nửa đường tròn tâm O có đường kính AB. Lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung KB (M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H và D. Đường thẳng BH căt nửa đường tròn tại điểm thứ hai N. Chứng minh 1) Tứ giác ACMD là tứ giác nội tiếp. 2)...
Đọc tiếp
GIÚP EM VỚI Ạ
Cho nửa đường tròn tâm O có đường kính AB. Lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung KB (M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H và D. Đường thẳng BH căt nửa đường tròn tại điểm thứ hai N. Chứng minh 1) Tứ giác ACMD là tứ giác nội tiếp. 2) CA.CB = CH.CD 3) Ba điểm A, N, D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DH
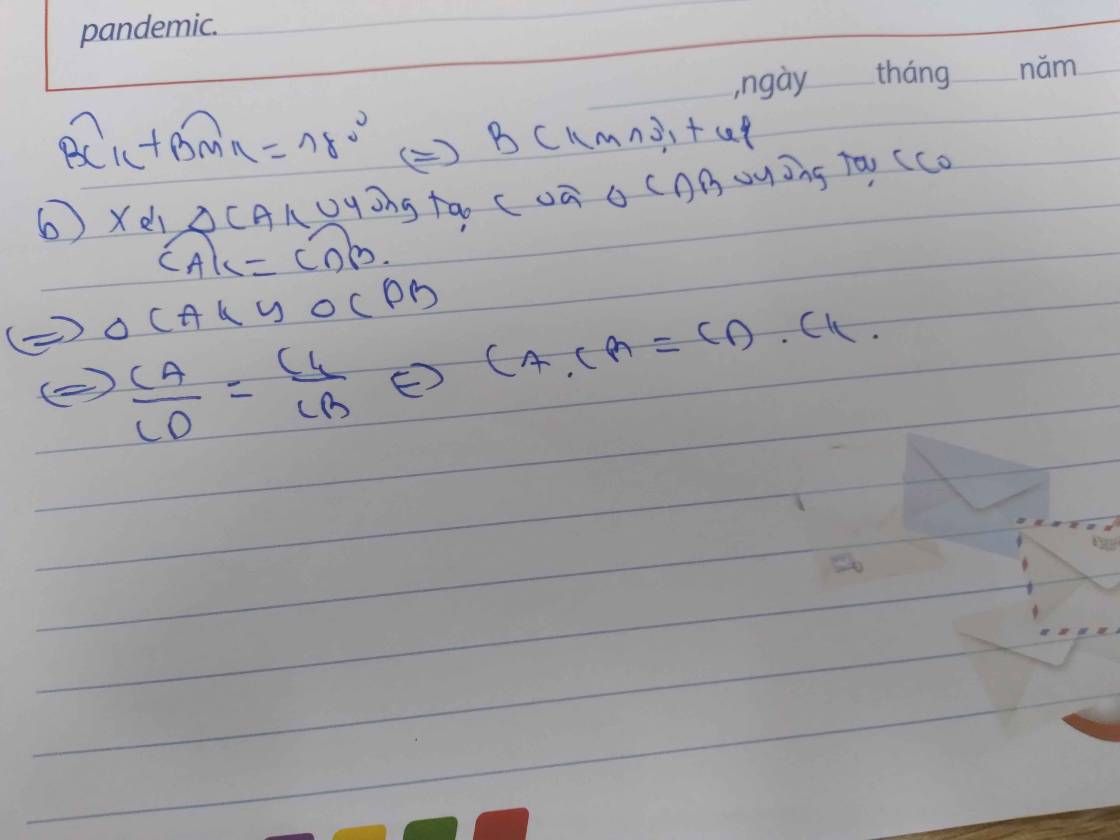
a, Xét (O) có :
^AMB = 900 ( góc nt chắn nửa đường tròn )
=> ^DMA = 900
Xét tứ giác ACMD có :
^ACD = ^DMA = 900
mà 2 góc này kề nhau, cùng nhìn cạnh AD
Vậy tứ giác ACMD là tứ giác nt 1 đường tròn
b, Vì tứ giác ACMD là tứ giác nt 1 đường tròn
=> ^HNM = ^HDM ( góc nt cùng chắn cung HM ) (1)
^BNM = ^MAB ( góc nt cùng chắn cung BM ) (2)
Từ (1) ; (2) => ^HDM = ^MAB
Xét tam giác CAH và tam giác CDB có :
^ACH = ^DCB = 900
^CAH = ^CDB ( cmt )
Vậy tam giác CAH ~ tam giác CDB (g.g)
=> CA/CD = CH/BC => AC.BC = CH.CD