Giúp mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)

mở bài là giới thiệu về cụ nha mn em viết lộn ạ
thân bài là đóng góp ạ

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi


a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B


A. MgSO4
- Liên kết ion được hình thành bởi cation kim loại Mg2+ và anion gốc axit SO42-
- Liên kết cộng hóa trị giữa S và O.
A: MgSO4
Liên kết ion giữa Mg2+ và SO42-, liên kết cộng hóa trị giữa S và O
 Ai giúp mình với ạ
Ai giúp mình với ạ


 các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ
các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ 
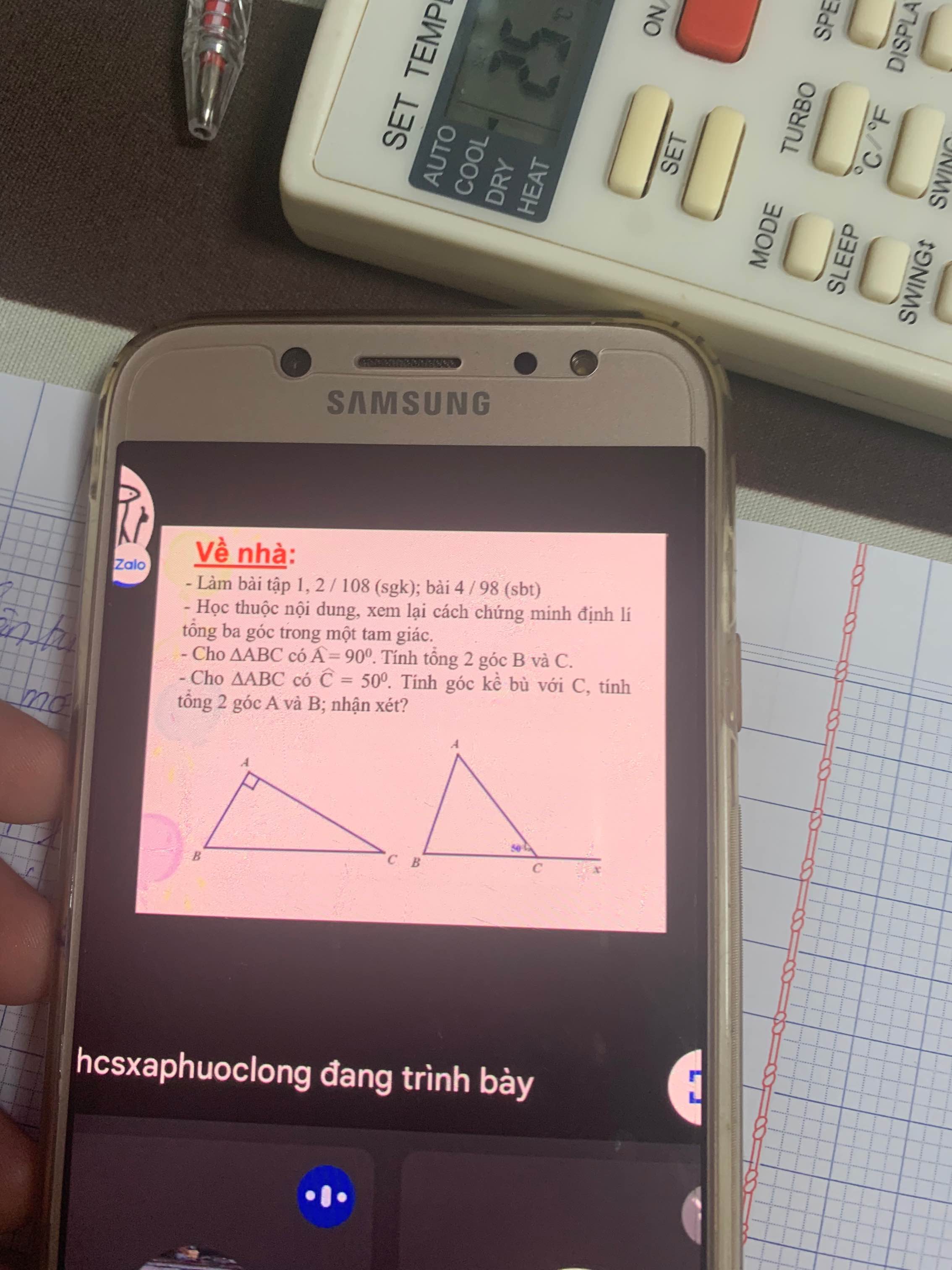
 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé 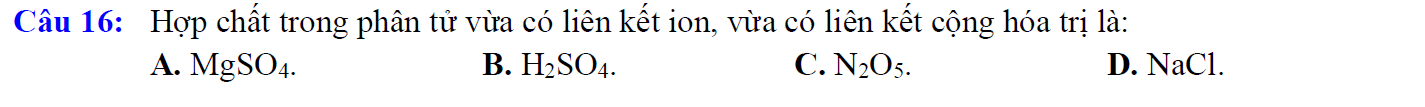 Giúp mình với ạ, mình đang cần gấp ạ
Giúp mình với ạ, mình đang cần gấp ạ
Answer:
Bài 1:
a. Ta xét vế trái:
\(\frac{5+3\sqrt{5}}{\sqrt{5}}+\frac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{5}+3\right)\)
\(=\frac{\sqrt{5}\left(\sqrt{5}+3\right)}{\sqrt{5}}+\frac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\sqrt{5}-3\)
\(=\sqrt{5}+3+\sqrt{3}-\sqrt{5}-3\)
\(=\sqrt{3}\)
b. Với \(a\ge1\)
\(P=a-\left(\frac{1}{\sqrt{a}-\sqrt{a-1}}-\frac{1}{\sqrt{a}+a-1}\right)\)
\(=a-\frac{\sqrt{a}+\sqrt{a-1}-\sqrt{a}+\sqrt{a-1}}{\left(\sqrt{a}-\sqrt{a-1}\right)\left(\sqrt{a}+\sqrt{a-1}\right)}\)
\(=a-\frac{2\sqrt{a-1}}{a-a+1}\)
\(=a-\frac{2\sqrt{a-1}}{1}\)
\(=a-2\sqrt{a-1}\)
\(=a-1-2\sqrt{a-1}+1\)
\(=\left(\sqrt{a-1}-1\right)\ge0\forall a\ge1\)
\(\Rightarrow P\ge0\)
Answer:
Bài 2:
\(3x+\sqrt{2}=2\left(x+\sqrt{2}\right)\)
\(\Rightarrow3x+\sqrt{2}=2x+2\sqrt{2}\)
\(\Rightarrow3x-2x=2\sqrt{2}-\sqrt{2}\)
\(\Rightarrow x=\sqrt{2}\)
\(3\sqrt{x-2}-\sqrt{x^2-4}=0\left(ĐK:-2\le x\le2\right)\)
\(\Rightarrow3\sqrt{x-2}=\sqrt{x^2-4}\)
\(\Rightarrow9\left(x-2\right)=x^2-4\)
\(\Rightarrow9x-2-x^2+4=0\)
\(\Rightarrow-x^2+9x+2=0\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{9+\sqrt{89}}{2}\text{(Loại)}\\x=\frac{9-\sqrt{89}}{2}\end{cases}}\)