cho đường tròn (O) và điểm A nằm ngoài đường tròn. vẽ tiếp tuyến AM,AN với đường tròn O (M,N thuộc O). qua A vẽ một đường thẳng cắt đường tròn O tại hai điểm B,C phân biệt (B nằm giữa A và C). gọi H là trung điểm của đoạn BC
a.cm tứ giác AMHN nội tiếp đường tròn
b.cm AN\(^2\)=AB.AC

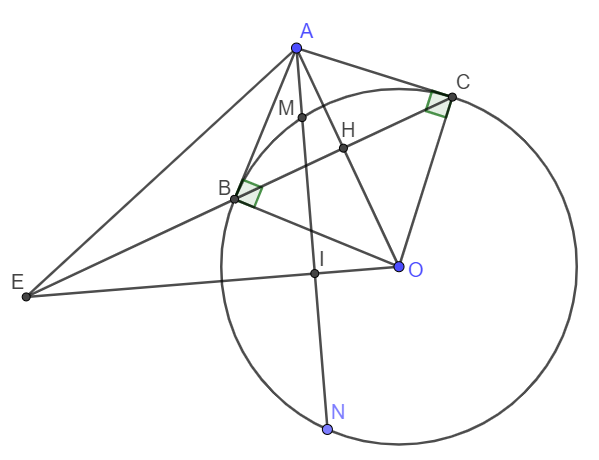
a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp
hay O,M,A,N cùng thuộc một đường tròn(1)
Xét tứ giác OHAN có
\(\widehat{OHA}+\widehat{ONA}=180^0\)
Do đó: OHAN là tứ giác nội tiếp
hay O,H,A,N cùng thuộc một đường tròn(2)
Từ (1) và (2) suy ra O,H,M,A,N cùng thuộc một đường tròn
hay AMHN là tứ giác nội tiếp
b: Xét ΔANB và ΔACN có
\(\widehat{CAN}\) chung
\(\widehat{ANB}=\widehat{ACN}\)
Do đó:ΔANB∼ΔACN
Suy ra: AN/AC=AB/AN
hay AN2=ABxAC