
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.

Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
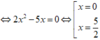
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()

Từ giả thiết: \(\int f\left(x\right).e^{2x}dx=x.e^x+C\)
Đạo hàm 2 vế:
\(\Rightarrow f\left(x\right).e^{2x}=e^x+x.e^x\)
\(\Rightarrow f\left(x\right)=\dfrac{e^x+x.e^x}{e^{2x}}=\dfrac{x+1}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2.e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}-2\int f\left(x\right).e^{2x}dx=\left(\dfrac{x+1}{e^x}\right)e^{2x}-2.x.e^x+C\)
\(=\left(1-x\right)e^x+C\)

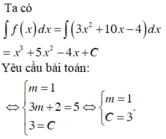
Vậy m =1 là giá trị cần tìm thỏa mãn yêu cầu bài toán.
Đáp án C

\(h\left(x\right)=x^2-4x+5+m\)
\(g\left(x\right)=\left|h\left(x\right)\right|=\left|f\left(x\right)+m\right|=\left|x^2-4x+5+m\right|\)
\(h\left(0\right)=5+m;h\left(4\right)=5+m;h\left(2\right)=1+m\)
TH1: \(1+m>0\Leftrightarrow m>-1\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
TH2: \(5+m< 0\Leftrightarrow m< -5\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
TH3: \(5+m>0>1+m\Leftrightarrow-5< m< -1\)
Nếu \(5+m< -1-m\Leftrightarrow m< -3\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
Nếu \(5+m=-1-m\Leftrightarrow m=-3\)
\(max=5+m=2\ne9\)
\(\Rightarrow m=-3\) không thỏa mãn yêu cầu bài toán
Nếu \(5+m>-1-m\Leftrightarrow m>-3\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
Vậy \(m=4;m=-10\)
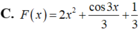
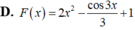
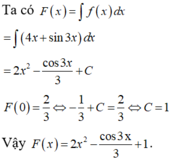
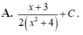
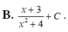
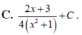
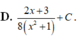

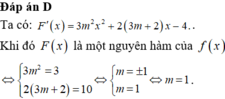
bài giải
\(f\left(x\right)=4x^5-\frac{1}{x}+2021\)
\(\int f(x)=\frac{4}{6}x^6-lnx+2021x\)
\(\int f(x)=\frac{2}{3}x^6-lnx+2021x\)