Cho tam giác ABC có \(\widehat{A}\)= 60o; \(\widehat{B}\)= 80o và có phân giác AD
a) So sánh các cạnh của tam giác ADC
b) So sánh các cạnh của tam giác ADB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
MH
3 tháng 2 2021
Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).
CM
22 tháng 1 2019
Ta có ∠C = 180o - 60o - 30o = 90o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn C
CM
22 tháng 12 2017
Áp dụng định lý Sin trong tam giác ABC ta có:
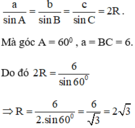
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.
CM
22 tháng 5 2019
Ta có ∠C = 180o - 30o - 60o = 90o
Tam giác ABC vuông tại C nên trực tâm tan giác ABC là điểm C.
Chọn C
4 tháng 8 2021
Đề thiếu dữ kiện bạn nhé, chỉ tính được tổng của góc D và góc C thôi.
thôi nha mik tự làm đc r