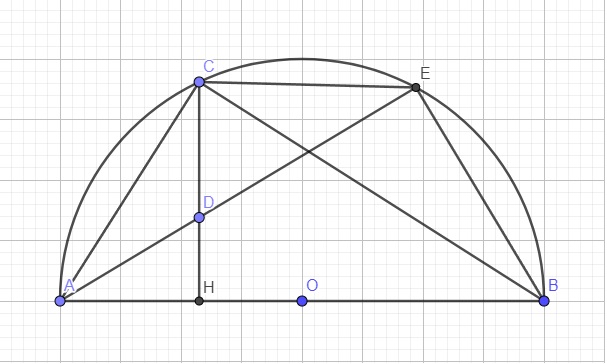
Cho đường tròn tâm O đường kính AB, qua một điểm H bất kỳ thuộc đoạn OA (H khác O và A) kẻ dây cung CD vuông góc với AB. Gọi M,N,P lần lượt là trung điểm các đoạn OB, BC và HB.
Chứng minh bốn điểm C,H,O,N cùng thuộc một đường tròn.
Kẻ đường thẳng qua M vuông góc với AB, cắt tia ON tại K, lấy S đối xứng với O qua K. Chứng minh rằng SB là tiếp tuyến của đường tròn (O).
Đường tròn đường kính CH cắt CP tại E. Lấy điểm F đối xứng với C qua A. Chứng minh rằng AH.HB=CE.CP và ba điểm E, H, F thẳng hàng.