Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B

Suy ra A, C sai
Kiểm tra thấy x = 0 không phải là nghiệm
của phương trình đã cho, suy ra D sai.
Vậy chỉ có B đúng.

Xét hàm số m sin 2 x + sin x - cos x = 0
Rõ ràng f(x) là hàm số liên tục trên R cho nên f(x) liên tục trong đoạn - π 2 ; π 2
Ta có f π 2 = 1 > 0 , f - π 2 = - 1 < 0 ∀ m (với mọi m).
Suy ra f - π 2 . f π 2 < 0 ∀ m
Do đó theo định lí trung gian phương trình đã cho có nghiệm - π 2 ; π 2
Suy ra A, C sai
Kiểm tra thấy x = 0 không phải là nghiệm của phương trình đã cho, suy ra D sai.
Vậy chỉ có B đúng.
Đáp án B

Đáp án C
Phương trình
sin x − 1 cos 2 x − cos x + m = 0 ⇔ sin x = 1 m = cos x − cos 2 x ⇔ x = π 2 + k 2 π 1 m = cos x − cos 2 x 2
Vì x ∈ 0 ; 2 π nên
0 ≤ π 2 + k 2 π ≤ 2 π ⇔ − 1 4 ≤ k ≤ 3 4 ⇒ k = 0 ⇒ x = π 2
Để phương trình đã cho có 5 nghiệm thuộc đoạn 0 ; 2 π ⇔ 2 có 4 nghiệm phân biệt thuộc 0 ; 2 π
Đặt t = cos x ∈ − 1 ; 1 , khi đó 2 ⇔ t 2 − t + m = 0 có 2 nghiệm phân biệt t 1 , t 2 thỏa mãn − 1 < t 1 ; t 2 < 1
⇔ t 1 + 1 t 2 + 1 > 0 t 1 − 1 t 2 − 1 > 0 Δ = − 1 2 − 4 m > 0 ⇔ t 1 t 2 + t 1 + t 2 + 1 > 0 t 1 t 2 − t 1 + t 2 + 1 > 0 − 4 m − 1 < 0 ⇔ 0 < m < 1 4
Vậy m ∈ 0 ; 1 4

Đáp án C
sin x − 1 cos 2 x − cos x + m = 0 ⇔ sin x = 1 1 cos 2 x − cos x + m = 0 2
Trong 0 ; 2 π thì phương trình (1) chỉ có 1 nghiệm x = π 2 nên để phương trình ban đầu có 4 nghiệm thì phương trình 2 phải có 4 nghiệm phân biệt tức là phương trình t 2 − t + m = 0 * phải có 2 nghiệm trong khoảng − 1 ; 1 và khác 0
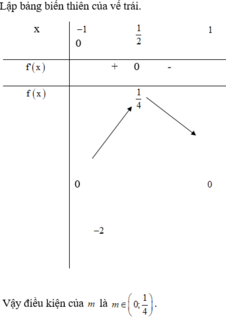
(*) ⇔ m = t − t 2 . Lập bảng biến thiên của vế trái.
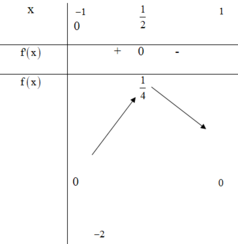
Vậy điều kiện của m là m ∈ 0 ; 1 4 .

Đáp án B.
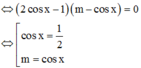
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
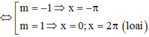
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
![]()
Vậy m= -1; m=0.

Đặt t = sin x + cos x − 2 ≤ t ≤ 2 ⇒ sin x cos x = t 2 − 1 2 .
Phương trình trở thành t 2 − 1 2 − t + m = 0 ⇔ − 2 m = t 2 − 2 t − 1 ⇔ t − 1 2 = − 2 m + 2 .
Do − 2 ≤ t ≤ 2 ⇒ − 2 − 1 ≤ t − 1 ≤ 2 − 1 ⇔ 0 ≤ t − 1 2 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm
⇔ 0 ≤ − 2 m + 2 ≤ 3 + 2 2 ⇔ − 1 + 2 2 2 ≤ m ≤ 1 → m ∈ ℤ m ∈ − 1 ; 0 ; 1 .
Chọn đáp án C.