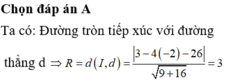Trên mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx - 1 (m ≠ 0). Tìm m để đường thẳng (d) tiếp xúc với đường tròn có tâm tại gốc tọa độ O và bán kính R = \(\dfrac{1}{\sqrt{10}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(m=1\Leftrightarrow y=1\Leftrightarrow\) Khoảng cách từ đường thẳng tới Ox là \(1\ne\sqrt{2}\) (loại)
Với \(m=0\Leftrightarrow y=-x\) là đt đi qua gốc tọa độ, k/c từ đường thẳng tới Ox là \(0\ne\sqrt{2}\) (loại)
Với \(m\ne1;m\ne0\)
PT giao Ox: \(\left(m-1\right)x+m=0\Leftrightarrow x=\dfrac{m}{1-m}\Leftrightarrow A\left(\dfrac{m}{1-m};0\right)\Leftrightarrow OA=\left|\dfrac{m}{1-m}\right|\)
PT giao Oy: \(y=m\Leftrightarrow B\left(0;m\right)\Leftrightarrow OB=\left|m\right|\)
Để đường thẳng là tiếp tuyến của \(\left(O;\sqrt{2}\right)\) thì khoảng cách từ O đến đường thẳng bằng độ dài bán kính
Gọi H là hình chiếu từ O đến đường thẳng \(\Leftrightarrow OH=\sqrt{2}\)
Áp dụng HTL: \(\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{OH^2}\)
\(\Leftrightarrow\left(\dfrac{1-m}{m}\right)^2+\dfrac{1}{m^2}=\dfrac{1}{2}\\ \Leftrightarrow\dfrac{m^2-2m+2}{m^2}=\dfrac{1}{2}\\ \Leftrightarrow2m^2-4m+4=m^2\\ \Leftrightarrow m^2-4m+4=0\\ \Leftrightarrow m=2\)
Vậy m=2 thỏa đề

Gọi I a ; - a a > 0 thuộc đường thẳng y = - x
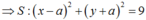
(S) tiếp xúc với các trục tọa độ
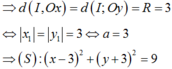
Chọn B.

a.
\(R=d\left(A;d\right)=\dfrac{\left|3+1-2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Phương trình đường tròn:
\(\left(x-3\right)^2+\left(y-1\right)^2=2\)
b.
Tiếp tuyến d' qua O nên có dạng: \(ax+by=0\)
d' tiếp xúc (C) nên \(d\left(A;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\Leftrightarrow\left(3a+b\right)^2=2a^2+2b^2\)
\(\Leftrightarrow7a^2+6ab-b^2=0\Rightarrow\left(a+b\right)\left(7a-b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a+b=0\\7a-b=0\end{matrix}\right.\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;7\right)\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}x-y=0\\x+7y=0\end{matrix}\right.\)
c.
Gọi M là trung điểm EF
\(\Rightarrow AM\perp EF\Rightarrow AM=d\left(A;d\right)=\sqrt{2}\)
\(S_{AEF}=\dfrac{1}{2}AM.EF=6\Rightarrow AM.EF=12\)
\(\Rightarrow EF=\dfrac{12}{\sqrt{2}}=6\sqrt{2}\)
\(\Rightarrow EM=\dfrac{EF}{2}=3\sqrt{2}\)
Áp dụng Pitago:
\(R'=AE=\sqrt{EM^2+AM^2}=2\sqrt{5}\)