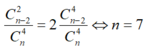Hàng năm cứ vào tháng 1 đầu năm, Thành Phố ABC tổ chức cuộc thi chọn đội tuyển về tin học tham dự kì thi chọn học sinh giỏi cấp tỉnh. Mỗi đội gồm ba học sinh. Theo truyền thống, các đối thủ cạnh tranh tốt nhất của Thành Phố là nữ sinh, và họ đông hơn nam sinh một cách đáng kể. Năm nay, các chàng trai đã lên tiếng và một quy tắc được đưa ra là mỗi đội phải bao gồm đúng một nam sinh và hai nữ sinh. Để giảm bớt áp lực lên kì thi, Thành phố quyết định cử đi KK bạn học sinh tham dự kì thi lập trình quốc tế online, KK thi sinh này sẽ không tham gia vào vòng loại chọn đội tuyển nữa. Cho biết số thí sinh nữ là MM, số thi sinh nam là NN, số thí sinh được cử đi tham dự kì thi lập trình quốc tế là KK. Yêu cầu: Cho biết M, NM,N và KK bạn hãy lập trình giúp Thành phố xác định số đội tuyển nhiều nhất mà Thành Phố có thể chọn để tham dự kì thi học sinh giỏi cấp tỉnh. Ví dụ, nếu M là 6, N là 3 và K là 2, Thành Phố có thể cử một nữ và một nam đi thi kì thi lập trình quốc tế online, để lại cho anh ta 5 cô gái và 2 cậu bé. Sau đó, có thể chọn ra hai đội từ họ (còn lại một cô gái không có đội). mô tả đầu vào Một dòng duy nhất ghi ba số nguyên M, N, KM,N,K (0\leq M, N \leq 100; 0 \leq K \leq M+N0≤M,N≤100;0≤K≤M+N) Mô tả đầu ra Ghi một dòng duy nhất là số đội lớn nhất mà thành phố có thể chọn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
The đề bài ta có C n − 2 2 C n 4 = 2 C n − 2 4 C n 4 ⇔ n = 7 .

Tham khảo:
Gọi số học sinh đạt giải cả 3 môn là a (học sinh)
Gọi số học sinh đạt giải cả 2 môn là b (học sinh)
Gọi số học sinh chỉ đạt giải 1 môn là c (học sinh)
Tổng số giải đạt được là: 3 x a + 2 x b + c = 15 (giải).
Vì tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c.
Vì bất kỳ 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ.
Do vậy b= 3.
Giả sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là:
3 x 2 + 2 x 3 + 4 = 16 > 15 (loại). Do đó a < 2, nên a = 1.
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12.
Nếu b = 3 thì c = 12 - 2 x 3 = 6 (đúng).
Nếu b = 4 thì c = 12 - 2 x 4 = 4 (loại vì trái với điều kiện b < c)
Vậy có 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải.
Đội tuyển đó có số học sinh là: 1 + 3 + 6 = 10 (bạn).

Gọi số học sinh đạt giải cả 3 môn là a ( học sinh ). Gọi số học sinh đạt giải cả 2 môn là b ( học sinh ). Gọi số học sinh chỉ đạt giải 1 môn là c ( học sinh ).
Tổng số giải đạt được là: 3 x a + 2 x b + c = 15 giải.
Vì tổng số số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c. Vì bất kì 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ
Do vậy b = 3
Gỉa sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là: 3 x 2 + 2 x 3 + 4 = 16 > 15 ( loại ).
Do đó a < 2, nên a = 1
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12
Nếu b = 3 thì c = 12 - 2 x 3 = ( đúng )
Nếu b = 4 thì c = 12 - 2 x 4 = 4 ( loại vì trái với điều kiện b < c)
Vậy 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải
Đội tuyển đó có số học sinh là: 1 + 3 + 6 = 10 ( bạn)
Bài giải:
Gọi số học sinh đạt giải cả 3 môn là a (học sinh)
Gọi số học sinh đạt giải cả 2 môn là b (học sinh)
Gọi số học sinh chỉ đạt giải 1 môn là c (học sinh)
Tổng số giải đạt được là:
3 x a + 2 x b + c = 15 (giải).
Vì tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c.
Vì bất kỳ 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ.
Do vậy b= 3.
Giả sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là:
3 x 2 + 2 x 3 + 4 = 16 > 15 (loại). Do đó a < 2, nên a = 1.
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12.
Nếu b = 3 thì c = 12 - 2 x 3 = 6 (đúng).
Nếu b = 4 thì c = 12 - 2 x 4 = 4 (loại vì trái với điều kiện b < c)
Vậy có 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải.
Đội tuyển đó có số học sinh là:
1 + 3 + 6 = 10 (bạn).

Đề thi chọn hs giỏi cấp huyện lớp 9 môn Sinh
https://dethihsg.com/tag/de-thi-hoc-sinh-gioi-mon-sinh-hoc-lop-9-co-dap-an/
Đề thi chọn đội dự tuyển tỉnh lớp 9 môn Sinh
https://dethi.violet.vn/present/show/entry_id/12187506
Cái đầu tiên tha hồ bn lựa nhé