Cho A=1+x+x2+...+xn. CMR: Với mọi số nguyên x thì xn+1-1 ⋮ x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
21 tháng 1 2022
Lời giảiL
$A=1+x+x^2+...+x^n$
$xA=x+x^2+x^3+...+x^n+x^{n+1}$
$\Rightarrow xA-A=(x+x^2+x^3+...+x^{n+1})-(1+x+x^2+...+x^n)$
Hay $A(x-1)=x^{n+1}-1$
$\Rightarrow A=\frac{x^{n+1}-1}{x-1}$ với $x$ nguyên dương khác $1$
Vì $A$ nguyên với mọi $x$ nguyên dương, $n$ tự nhiên nên $\frac{x^{n+1}-1}{x-1}$ nguyên
$\Rightarrow x^{n+1}-1\vdots x-1$ (đpcm)
MN
23 tháng 4 2019
Bài 1 :
8x - 0,4 = 7,8*x + 402
8x - 7,8*x = 402 + 0,4
0,2*x = 402,04
x= 402,04 : 0,2
x = 2012
MN
23 tháng 4 2019
Bài 2
Theo bài ra , số học sinh lớp 6A bằng 1/2 tổng số học sinh hai lớp 6B và 6C
=> Số học sinh lớp 6A bằng 1/3 số học sinh của cả 3 lớp
Số học sinh lớp 6A là :
120 x 1/3 = 40 học sinh
Tổng số học sinh lớp 6B và 6C là :
120 - 40 = 80 học sinh
Số học sinh lớp 6B là :
( 80 - 6 ) : 2 = 37 học sinh
Số học sinh lớp 6C là :
37 + 6 = 43 học sinh
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
CM
11 tháng 4 2017
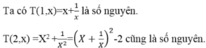
\Ta sẽ chứng minh T(1,x) là số nguyên
Thật vậy, áp dụng phép chứng minh quy nạp, Ta có:
Bước cơ sở: T(1,x) là số nguyên. Khẳng định đúng với n=1
Bước quy nạp: Giả sử T(n,x) là số nguyên với mọi n≥1. Ta sẽ chứng minh T(n+1,x) cũng là số nguyên
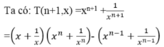
=T(1,x).T(n,x) – T(n-1,x).
Theo giả thuyết quy nạp, Ta có T(1,x),T(n,x), T(n-1,x) là các số nguyên nên T(n+1,x) là số nguyên
Chọn C
8 tháng 2 2016
a.đặt a+15=b2;a-1=c2
=>(a+15)-(a-1)=b2-c2=(b+c)(b-c)
=>(b+c)(b-c)=16
ta có 2 nhận xét:
*(b+c)-(b-c)=2c là 1 số chẵn nên 2 số b+c và b-c là 2 số cùng tính chẵn lẻ.Mà 16 là số chẵn nên 2 số b+c và b-c cùng chẵn.
*b+c>b-c(vì a là số tự nhiên)
=>b+c=8 và b-c=2 =>b=(8+2):2=5
vậy a+15=52=>a=10
PT
1
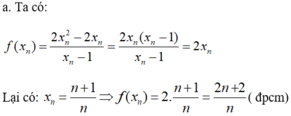
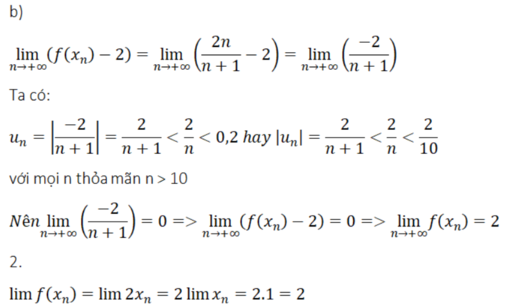
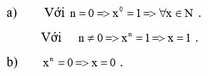
hdt là j
HĐT nào anh : Cái này á: xn-yn=(x-y)(xn-1+xn-2y+...+xyn-2+yn-1)?