Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b, Còn câu b thì có thể cần nhé :
Theo câu a ta có : AH=AK ( tam giác AHM=AKM )
Mà AB=AC ( ABC cân ở A )
=> HB=CK
Xét tam giác BHC và CKB có :
góc HBC=KCB ( ABC cân ở A )
HB=CK
BC chung
=> hai tam giác bằng nhau ( cạnh-góc-cạnh )
=> CH=BK.
mình chỉ giúp ý d theo mong muốn của bạn thôi :)
Có : AH = AK ( cái này bạn chứng minh ở câu trên chưa mình không biết; nếu chưa thì bạn chứng minh đi nhé )
=> A thuộc đường trung trực của HK
và MH=MK
=> M thuộc đường trung trực của HK
=> AM là đường trung tực của HK
=> AM ⊥ HK
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) =90o
Cạnh huyền AM chung
∠(HAM) =∠(KAM) (gt)
⇒ ΔAHM= ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
a:
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
a. Ta có: AB = AC
\(\Rightarrow\Delta ABC\) cân tại A.
Mà tia phân giác của góc cân đồng thời cắt cạnh đối tại trung điểm của nó.
Vậy: BM = MC.
b. Xét 2\(\Delta\): \(\Delta ABM\) và \(\Delta ACM\) có:
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{BAM}=\widehat{CAM}\left(gt\right)\\AM.chung\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Vậy \(\widehat{AMB}=\widehat{AMC}\)
Mà: \(\widehat{BMC}=180^o\)
Vậy: \(\widehat{AMB}=90^o\) hay \(AM\perp BC\)
a) Xét tam giác ABM và tam giác ACM, ta có:
AB = AC (gt)
AM: cạnh chung
Góc BAM = góc CAM (do AM là tia phân giác của góc BAC)
=> tam giác ABM = tam giác ACM (c.g.c)
=> BM = MC (2 cạnh tương ứng) (đpcm)
b) Xét tam giác ABC, ta có:
AB = AC (gt)
=> tam giác ABC cân tại A
Mà AM là tia phân giác góc BAC
=> AM cũng là đường cao ứng với BC
=> AM vuông góc BC (đpcm)
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc BAC
hay góc BAM= góc CAM
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
hay ΔMHK cân tại M
d: Xét ΔAHK có AH=AK
nên ΔAHK cân tại A
e: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
mà AM là tia phân giác
nên AHMK là hình vuông
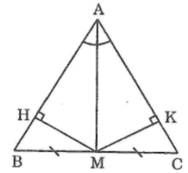
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM
Tham khảo:
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
ˆHAM=ˆKAMHAM^=KAM^
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM