Cho x + y = 1 và xy # 0.C/M:
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}+\frac{2\left(x-y\right)}{x^2y^2+3}=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TB
0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(6xy=x+y\ge2\sqrt[]{xy}\Rightarrow\sqrt{xy}\ge\dfrac{1}{3}\Rightarrow xy\ge\dfrac{1}{9}\Rightarrow\dfrac{1}{xy}\le9\)
\(M=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{xy+x}{1-xy}+1}{1+\dfrac{xy+x}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{x+1}{1-xy}}{\dfrac{x+1}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{1}{1-xy}+\dfrac{1}{1+xy}}{\dfrac{1}{1-xy}-\dfrac{1}{1+xy}}\)
\(M=\dfrac{1+xy+1-xy}{1+xy-1+xy}=\dfrac{2}{2xy}=\dfrac{1}{xy}\le9\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{3}\)
20 tháng 7 2019
\(1,A=\frac{1}{x^2+y^2}+\frac{1}{xy}=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\)
\(\ge\frac{4}{\left(x+y^2\right)}+\frac{1}{\frac{\left(x+y\right)^2}{2}}\ge\frac{4}{1}+\frac{2}{1}=6\)
Dấu "=" <=> x= y = 1/2
20 tháng 7 2019
\(2,A=\frac{x^2+y^2}{xy}=\frac{x}{y}+\frac{y}{x}=\left(\frac{x}{9y}+\frac{y}{x}\right)+\frac{8x}{9y}\ge2\sqrt{\frac{x}{9y}.\frac{y}{x}}+\frac{8.3y}{9y}\)
\(=2\sqrt{\frac{1}{9}}+\frac{8.3}{9}=\frac{10}{3}\)
Dấu "=" <=> x = 3y
TB
3
13 tháng 10 2017
Theo bài ra ta có:
\(x^2y+xy^2+x+y=\left(x^2y+xy^2\right)+x+y\)
\(=xy\left(x+y\right)+x+y=x+y+x+y\)
\(\Rightarrow2\left(x+y\right)=16\Rightarrow x+y=16\div2=8\)
\(\Rightarrow\left(x+y\right)^2=8^2=64\)
\(\Rightarrow x^2+2xy+y^2=64\)
\(\Rightarrow x^2+2+y^2=64\)
\(\Rightarrow x^2+y^2=64-2=62\)
Vậy \(x^2+y^2=62\)
13 tháng 10 2017
\(x^2y+xy^2+x+y=16\)
\(\Leftrightarrow2x+2y=16\)
\(\Leftrightarrow x+y=8\)
Lại có\(x^2+y^2=\left(x+y\right)^2-2xy\)
\(=8^2-2\)
\(=62\)
Vậy\(x^2+y^2=62\)
TB
0
28 tháng 1 2022
\(xy\le\dfrac{\left(x+y\right)^2}{4}=\dfrac{1}{4}\)
\(\Rightarrow P=xy+\dfrac{1}{xy}=xy+\dfrac{1}{16xy}+\dfrac{15}{16xy}\ge2\sqrt{xy.\dfrac{1}{16xy}}+\dfrac{15}{16.\dfrac{1}{4}}=\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
\(min_P=\dfrac{17}{4}\Leftrightarrow x=y=\dfrac{1}{2}\)
DN
1
BT
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
\(P=\dfrac{x^3+y^3}{x^3y^3}=\dfrac{\left(x+y\right)\left(x^2+y^2-xy\right)}{x^3y^3}=\dfrac{x^2y^2\left(x+y\right)}{x^3y^3}=\dfrac{x+y}{xy}=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{x^2+y^2-xy}=\dfrac{4\left(x^2+y^2-xy\right)-3\left(x^2+y^2-2xy\right)}{x^2+y^2-xy}\)
\(=4-\dfrac{3\left(x-y\right)^2}{x^2+y^2-xy}\le4\)
\(P_{max}=4\) khi \(x=y=\dfrac{1}{2}\)
CM
8 tháng 10 2019
Đáp án B
Theo giả thiết có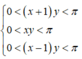 
và
Và thay vào đẳng thức điều kiện có:
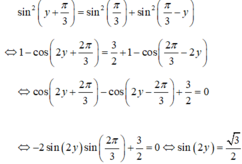
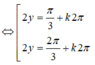
Đối chiếu với điều kiện nhận 
x=y-1 rồi thế từ từ vào