a) Xác định hệ số a của paradol y = a\(x^2\), biết rằng paradol đi qua A(-2;-2)
b) Tìm tọa độ của M thuộc paradol nói trên, biết rằng khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm giữa (P) và (d)
\(x^2=2x+3\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Delta=\left(-2\right)^2-4.1.\left(-3\right)=16>0\)
\(\Rightarrow x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-\sqrt{16}}{2.1}=-1\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{2+\sqrt{16}}{2.1}=3\)
Với x1 =-1 \(\Rightarrow\) y1 = (-1)2 =1 \(\Rightarrow\) A(-1;1)
x2 =3 \(\Rightarrow\)y2 =32 =9 \(\Rightarrow\)B(3;9)
Vậy tọa độ giao điểm là A(-1;1) và B(3;9)

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 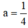
Vậy hàm số: 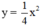
| x | -4 | -2 | 0 | 2 | 4 |
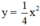 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
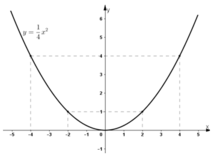

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 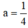
Vậy hàm số: 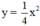
| x | -4 | -2 | 0 | 2 | 4 |
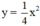 |
4 | 1 | 0 | 1 | 4 |
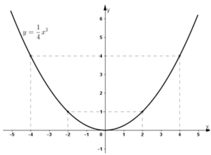
Đồ thị hàm số:

Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
Đồ thị của hàm số đi qua điểm A(2; 6) nên:
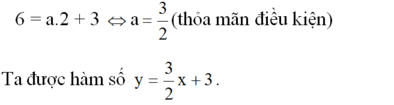

Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
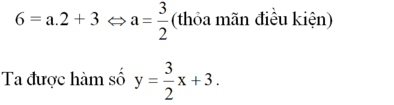
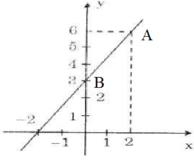
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số

Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:

dễ mà tự giải đi bạn ưi tui ko bít cách giải đâu nên đừn hỏi