Cứu em vs mng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
3 tháng 12 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
HN
2
29 tháng 4 2022
a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
29 tháng 4 2022
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)
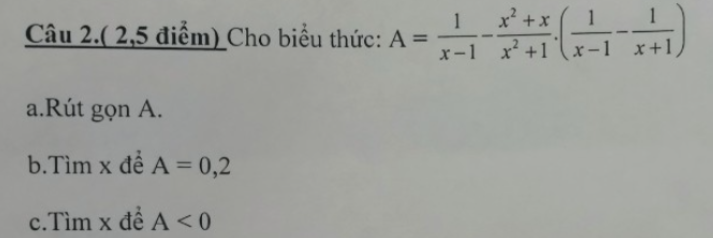
a) Cấu hình e của R: 1s22s22p63s1
b) R thuộc chu kì 3, nhóm IA, nguyên tố s
c) Do R có 1e lớp ngoài cùng => R có tính chất của kim loại
d) Cấu hình của X: 1s22s22p5
=> X là F(Flo)
Thanks bn nhiều