Cho định lý : Bất kì điểm nào năm trên đường trung trực của đoạn thẳng thẳng AB cũng cách đều hai đầu mút của đoạn thẳng đó
a/ Vẽ hình và viết GT & KL của định lý
b/ Chứng minh định lí
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

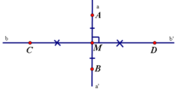
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.


1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
b: Gọi O là điểm nằm trên đường trung trực của AB
=>OH⊥AB tại H
=>H là trung điểm của AB
Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
HA=HB
Do đó: ΔOHA=ΔOHB
Suy ra: OA=OB