Hai tổ công nhân cùng làm chung một công việc thì sau 2 giờ 24 phút hoàn thành.
Trong thực tế, tổ 1 làm trong 2 giờ, sau đó tổ 2 hoàn thành nốt công việc còn lại trong 3 giờ.
Hỏi nếu làm riêng một mình thì mỗi tổ hoàn thành công việc đó trong bao lâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x(h) là thời gian tổ 1 hoàn thành công việc khi làm một mình
y(h) là thời gian tổ 2 hoàn thành công việc khi làm một mình
(Điều kiện: x>6; y>6)
Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{6}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)
Trong 12 giờ, tổ 1 làm được: \(\dfrac{12}{x}\)(công việc)
Trong 2 giờ, tổ 2 làm được: \(\dfrac{2}{y}\)(công việc)
Theo đề, ta có phương trình: \(\dfrac{12}{x}+\dfrac{2}{y}=1\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{12}{x}+\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{12}{x}+\dfrac{12}{y}=2\\\dfrac{12}{x}+\dfrac{2}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{y}=1\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=10\\\dfrac{1}{x}+\dfrac{1}{10}=\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{15}\\y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=15\\y=10\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 15 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 10 giờ để hoàn thành công việc khi làm một mình

Gọi thời gian làm riêng xong việc của tổ 1 là x>0 (giờ) và tổ 2 là y>0 giờ
Trong 1 giờ hai tổ lần lượt làm được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc
Do 2 tổ làm chung trong 8 giờ thì hoàn thành nên: \(8\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
Hai đội làm việc chung trong 6h và đội 1 làm việc 1 mình thêm 6h thì hoàn thành nên:
\(6\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+6.\dfrac{1}{x}=1\) \(\Leftrightarrow\dfrac{2}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)
Ta được hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\\\dfrac{2}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=24\\y=12\end{matrix}\right.\)

Gọi x(h) là thời gian tổ 1 hoàn thành công việc khi làm một mình
Gọi y(h) là thời gian tổ 2 hoàn thành công việc khi làm một mình
(Điều kiện: x>8; y>8)
Trong 1 giờ, đội 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, đội 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai đội làm được: \(\dfrac{1}{8}\)(công việc)
Do đó, ta có phương trình \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\)(1)
Trong 3 giờ, tổ 1 làm được: \(\dfrac{3}{x}\)(công việc)
Trong 10 giờ, tổ 2 làm được: \(\dfrac{10}{y}\)(công việc)
Theo đề, ta có phương trình: \(\dfrac{3}{x}+\dfrac{10}{y}=\dfrac{2}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\\\dfrac{3}{x}+\dfrac{10}{y}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{8}\\\dfrac{3}{x}+\dfrac{10}{y}=\dfrac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-7}{y}=\dfrac{-7}{24}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=24\\\dfrac{1}{x}+\dfrac{1}{24}=\dfrac{1}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{12}\\y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=24\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 12 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 24 giờ để hoàn thành công việc khi làm một mình

Đáp số: 144 giờ
Cho bạn biết trước kết quả nhé!
Câu hỏi của Nguyễn Thúy Hằng - Toán lớp 5 - Học toán với OnlineMath
Tham khảo

Một giờ cả 2 tổ làm được số công việc : 1 : 48 = 1/48 (công việc)
Giả sử tổ 1 cũng chỉ làm 24 giờ rồi nghỉ khi đó số công việc 2 tổ làm được : 1/48 x 24 = 1/2 (công việc)
Số giờ tổ 1 làm thêm để hết công việc : 60 - 24 = 36 (giờ)
36 giờ tổ 1 làm tương ứng số công việc : 1 - 1/2 = 1/2 (công việc)
Mình tổ 1 làm hết công việc cần số giờ : 36 x 2 = 72 (giờ)
1 giờ mình tổ 1 là được số công việc : 1 : 72 = 1/72 (công việc)
1 giờ tổ 2 làm được số công việc : 1/48 - 1/72 = 1/144(công việc)
Mình tổ 2 làm xong công việc hết số giờ : 1 : 1/144 = 144 (giờ)
**** giùm

Gọi năng suất của tổ 1 là x (x > 0, phần công việc/giờ)
Vì hai tổ sản xuất cùng làm chung công việc thì hoàn thành trong 2 giờ nên năng suất của tổ 2 là: ½ - x (phần công việc/giờ)
Thời gian tổ 1 làm 1 mình xong công việc là: 1/x (giờ)
Thời gian tổ 2 làm 1 mình xong công việc là: 1 1 2 - x (giờ)
Vì khi làm riêng, tổ một hoàn thành sớm hơn tổ hai là 3 giờ nên ta có phương trình:
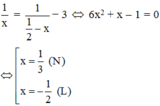
Vậy thời gian tổ 1 hoàn thành công việc một mình là 3 giờ
Đáp án: A