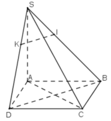
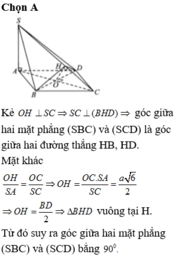
Cho hình chóp S.ABCD là hình thoi cạnh 3a , \(\widehat{BAD}=60^0\) và SC=SB=SD=\(a\sqrt{6}\) .Mặt phẳng (P) thay đổi nhưng luôn qua B và \(\perp\) với (SCD) .Gọi \(\varphi\) là góc giữa BD và (P) .Tính GTLN của \(sin\varphi\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}=60^0\Rightarrow\) các tam giác ABC và ACD là các tam giác đều
\(AH=AC\Rightarrow AH=AC=AB\Rightarrow\Delta HBC\) vuông tại B
\(\Rightarrow HB\perp BC\Rightarrow HB\perp AD\)
Qua H kẻ đường thẳng \(d\perp\left(ABCD\right)\Rightarrow S\in d\)
Gọi O là giao điểm AC và BD, do góc giữa (SBD) và đáy bằng 60 độ
\(\Rightarrow\widehat{SOH}=60^0\)
\(\Rightarrow SH=OH.tan60^0=\left(AH+AO\right).tan60=\left(a+\dfrac{a}{2}\right).tan60^0=\dfrac{3a\sqrt{3}}{2}\)
\(V_{S.ABCD}=\dfrac{1}{3}SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{3a\sqrt{3}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
b.
\(SC=\sqrt{SH^2+HC^2}=\sqrt{SH^2+\left(2AC\right)^2}=\dfrac{a\sqrt{43}}{2}\)
\(\Rightarrow M\) là trung điểm SC \(\Rightarrow AM\) là đường trung bình tam giác SHC
\(\Rightarrow\left\{{}\begin{matrix}AM||SH\Rightarrow AM\perp\left(ABCD\right)\\AM=\dfrac{1}{2}SH=\dfrac{3a\sqrt{3}}{4}\end{matrix}\right.\)
\(HD=\sqrt{OD^2+OD^2}=\sqrt{\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2}=a\sqrt{3}\)
\(\Rightarrow SD=\sqrt{SH^2+HD^2}=\dfrac{a\sqrt{39}}{2}\Rightarrow SN=\dfrac{1}{3}SD\Rightarrow ND=\dfrac{2}{3}SD\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}d\left(S;\left(MAD\right)\right)\)
Mà \(SH||\left(MAD\right)\Rightarrow d\left(S;\left(MAD\right)\right)=d\left(H;\left(MAD\right)\right)\)
Gọi E là giao điểm BH và AD, ta có:
\(\left\{{}\begin{matrix}HB\perp AD\left(cmt\right)\\AM\perp\left(ABCD\right)\Rightarrow AM\perp HB\end{matrix}\right.\) \(\Rightarrow HB\perp\left(MAD\right)\)
\(\Rightarrow HE=d\left(H;\left(MAD\right)\right)\)
\(HE=\dfrac{1}{2}HB=\dfrac{1}{2}HD=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}HE=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{AMND}=\dfrac{1}{3}.d\left(N;\left(MAD\right)\right).\dfrac{1}{2}AM.AD=\dfrac{a^3}{8}\)
CM
19 tháng 4 2019
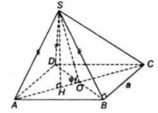
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
CM
21 tháng 1 2018
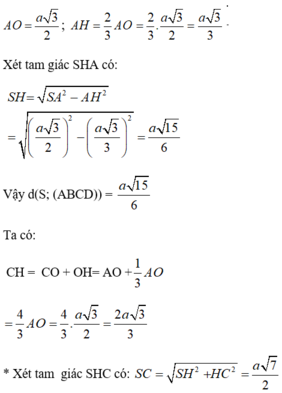
Đáp án C
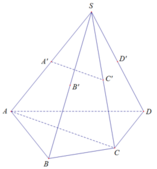
Mặt phẳng (P) đi qua A’ và song song AC
Trong mặt phẳng (SAC), ta có A’C’//AC (A’C’ là đường trung bình tam giác SAC)
⇒ (P) đi qua A’C’ cố định
