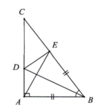
cho tam giác ABc có A=90 độ , trên cạnh BC lấy điểm E sao cho BA=BE. tia phân giác góc B cắt AC ở D . a. chứng minh: tam giác ABD = tam giác EBD b.chứng minh : DA=DE. c. tính số đo BED d.Xác định độ lớn góc B để EDB = EDC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
22 tháng 12 2021
Answer:
Phần c) thì nhờ các cao nhân khác thoii.
a) Ta xét tam giác ABD và tam giác EBD:
AB = EB (gt)
BD cạnh chung
\(\widehat{B_1}=\widehat{B_2}\)
Vậy tam giác ABD = tam giác EBD (c.g.c)
\(\Rightarrow DE=DA\)
b) Theo phần a), tam giác ABD = tam giác EBD
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\)
2 tháng 12 2018
HÌNH KO CHUẨN LẮM
a) Xét \(\Delta ABD-\Delta EBD\) có :
BA = BE
\(\widehat{ABD}=\widehat{EBD}\)( phân giác )
DB là cạnh chung
=> \(\Delta ABD=\Delta EBD\)(C,G,C)
b) theo câu a) 2 tam giác ... = nhau
=> DA = DE ( 2 cạnh tương ứng )
c) theo câu a) 2 tam giác ... = nhau
=> \(\widehat{BAD}=\widehat{BED}=90^o\)( 2 góc tương ứng )
d) xét 2 tam giác \(\Delta EDB-\Delta EDC\)CÓ:
BED = CED ( góc vuông )
DE là cạnh chung
Để 2 tam giác \(\Delta EDB=\Delta EDC\) thì
\(\widehat{EBD}=\widehat{C}\)
MÀ \(\widehat{EBD}=\frac{1}{2}B\)
vậy để 2 tam giác đó = nhau thì góc B phải gấp 2 lần góc C
30 tháng 12 2020
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
Vậy: \(\widehat{BED}=90^0\)
c) Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ΔBAD=ΔBED(cmt)
nên AD=ED(hai cạnh tương ứng)
hay D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
hay BD⊥AE(đpcm)
C
30 tháng 12 2020
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
ˆABD=ˆEBDABD^=EBD^(BD là tia phân giác của ˆABEABE^)
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên ˆBAD=ˆBEDBAD^=BED^(hai góc tương ứng)
mà ˆBAD=900BAD^=900(ΔABC vuông tại A)
nên ˆBED=900BED^=900
Vậy: ˆBED=900BED^=900
c) Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ΔBAD=ΔBED(cmt)
nên AD=ED(hai cạnh tương ứng)
hay D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
hay BD⊥AE(đpcm)
