Cho tam giác ABC vuông tại A. Từ trung điểm D của cạnh BC kẻ DE, DF lần lượt vuông góc với AB, AC (E thuộc AB, F thuộc AC).
a) Chứng minh: tứ giác AEDF là hình chữ nhật.
b) Gọi I là điểm đối xứng của D qua E. Chứng minh: tứ giác AIBD là hình thoi.
c) Gọi O là trung điểm của EF. Chứng minh: ba điểm I, O, C thẳng hàng.

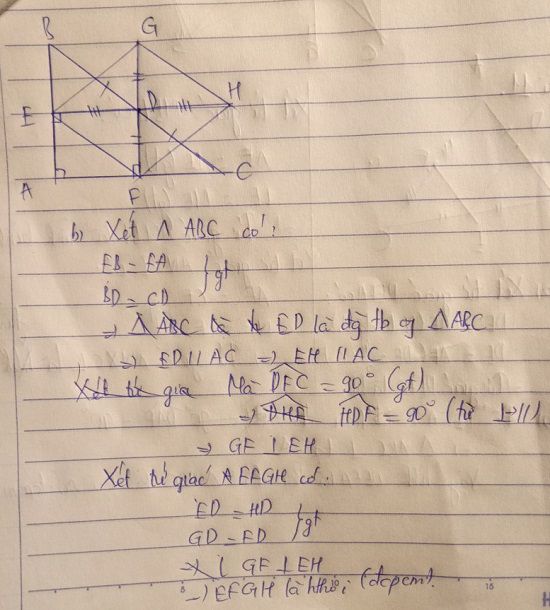

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi