cho tam giác abc có ab=ac tia phân giác của góc a cắt bc tại d
a) chứng minh \(_{\Delta}\)ABD=\(\Delta\)ACD
b) kẻ DH vuông góc với AB (H\(\in\)AB) DK vuông góc với ac k\(\in\)AC chứng minh AH=AK
C) CHỨNG MINH ĐƯỜNG THẲNG HK SONG SONG VỚI BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD

b: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔADH=ΔADK
Suy ra: AH=AK

Hướng dẫn bạn làm nhé, bài này cũng đơn giản thôi :P
a/ \(\Delta ABD=\Delta ACD\left(c.g.c\right)\)
b/ \(\Delta AHD=\Delta AKD\left(canhhuyen...gocnhon\right)\)
\(\Rightarrow HD=KD\)
c/ tự làm

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: DB=DC(hai cạnh tương ứng)
b) Xét ΔDBH vuông tại H và ΔDCK vuông tại K có
DB=DC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDBH=ΔDCK(cạnh huyền-góc nhọn)
Suy ra: DH=DK(hai cạnh tương ứng)

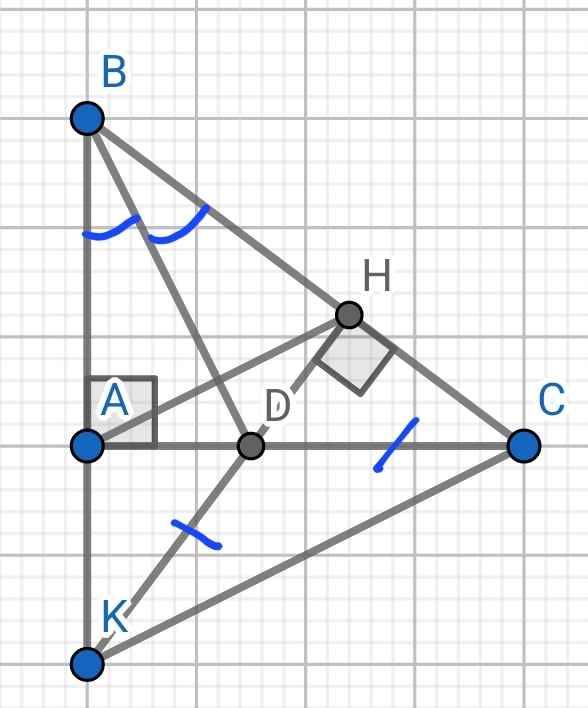
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng

Mình làm câu A thôi nha:
Xét tam giác ADB và tam giác ADC
Ta có:AB=AC (gt)
góc A1=A2 (gt)
AD là cạnh chung
=>tam giác ADB=tam giác ADC (cạnh-góc-cạnh)
![]()
![]()
![]()
Xét AHD và AKD lần lượt vuông tại H,K có:
AD: cạnh chung
HAD = KAD ( vì AD là tia phân giác góc A)
Suy ra AHD=AKD(ch-gn)
Do đó AH=AK ( 2 cạnh tương ứng)

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
ˆBAD=ˆCADBAD^=CAD^(AD là tia phân giác của ˆBACBAC^)
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: DB=DC(hai cạnh tương ứng)
b) Xét ΔDBH vuông tại H và ΔDCK vuông tại K có
DB=DC(cmt)
ˆB=ˆCB^=C^(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDBH=ΔDCK(cạnh huyền-góc nhọn)
Suy ra: DH=DK(hai cạnh tương ứng)
mình ko biết có đúng ko nx

Một trường THCS. Tổng kết cuối học kì I, tổng số học sinh giỏi và khá nhiều hơn sô học sinh đạt loại trung bình là 60 học sinh. Biết rằng số học sinh giỏi, khá, trung bình lần lượt tỉ lệ với 2: 5: 6. Tính số học sinh mỗi loại ?
b: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔADH=ΔADK
Suy ra: AH=AK
a: Ta có: \(\widehat{BMA}+\widehat{ABM}=90^0\)
\(\widehat{BMD}+\widehat{DBM}=90^0\)
mà \(\widehat{ABM}=\widehat{DBM}\)
nên \(\widehat{BMA}=\widehat{BMD}\)
c: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
Suy ra: MA=MD
Xét ΔAME vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMC}\)
Do đó: ΔAME=ΔDMC