Số táo ở rổ thứ nhất bằng 4/5 số táo ở rổ thứ hai. Nếu chuyển 30 quả từ giở thứ nhất sang giỏ hai thì giỏ thứ nhất bằng 19/17 rổ thứ hai. Tính số táo ở hai rổ lúc ban đầu
(Mik còn gấp) Mong các bạn trả lời hộ mik nhé. Cảm ơn các bạn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2023
Gọi số táo ở rổ 2 là x
=>Số táo ở rổ 1 là 4/5x
Theo đề, ta có: 4/5x-30=19/17(x+30)
=>4/5x-30=19/17x+570/17
=>-27/85x=1080/17
=>x=-200
=>Đề sai rồi bạn
30 tháng 7 2015
nếu chuyển ở rổ 2 sang rổ 1 thì số táo ko thay đổi
số táo ở rổ 1 lúc đầu bằng 2/3 số táo ở rổ 2 tức là bằng 2/5 số táo trong cả 2 rổ
số táo ở rổ 1 lúc sau bằng 18/17 số táo ở rổ 2 tức là bằng 18/35 số táo ở trong 2 rổ
p/s chỉ 32 quả táo là:
18/35 - 2/5 = 4/35( số táo ở cả 2 rổ)
số táo trong 2 rổ là
32 : 4/35 = 280 (quả)
số táo ở rổ 1lúc đầu là
280 . 2/5 = 112(quả)
số táo ở rổ 2 lúc đầu là
280 - 112 = 168 ( quả)
PT
4 tháng 4 2016
Gọi a là số táo ban đầu ở rổ 1
b là số táo ban đầu ở rổ 2
Lúc đầu số táo ở rổ 1 bằng 2/3 số táo ở rổ 2 nên ta có: a=\(\frac{2}{3}\)b (1)
Chuyển 32 quả táo từ rổ 2 sang rổ 1 thì số táo ở rổ 1 bằng 18/17 số táo ở rổ 2 nên ta có: (a+32)=\(\frac{18}{17}\)(b-32) (2)
Thế (1) vào (2) ta được: ( \(\frac{2}{3}\)b+32)=\(\frac{18}{17}\)(b-32)
<=> \(\frac{18}{17}\) b - \(\frac{2}{3}\)b = 32+\(\frac{576}{17}\)
<=> \(\frac{20}{51}\)b=\(\frac{1120}{17}\) <=> b=168Thế b=168 vào (1) suy ra a=112Vậy: Số táo ban đầu ở rổ 1 là 112 quả Số táo ban đầu ở rổ 2 là 168 quả
CM
25 tháng 5 2019
Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
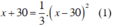
Giải phương trình (1):
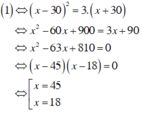
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.
19 tháng 2 2021
- Gọi số trứng ban đầu ở mỗi rổ là x, y ( quả, \(x,y\in N\) * )
Theo bài ra tổng số quả 2 rổ là 80 quả .
=> x + y = 80 ( I )
Ta lại có : Nếu chuyển ở rổ thứ nhất sang rổ thứ hai 5 quả thì số trứng ở rổ thứ nhất bằng 3/5 số trứng ở rổ thứ hai .
Nên ta có phương trình : \(x-5=\dfrac{3}{5}\left(y+5\right)\)
=> 5x - 25 = 3y + 15
=> 5x - 3y = 40 ( II )
- Từ ( I ) và ( II ) ta được hệ phương trình .
- Giair hệ phương trình ta được : x = 35, y = 45 ( TM )
Vậy ...
