b. Chứng minh AB = IK Câu 7: Cho hinh thoi ABCD. gọi I là giao điểm của hai đường chéo. Vẽ đường thăng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau ở K. a. Chứng minh tứ giác IBKC là hình chữ nhật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2022
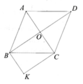
a: Xét tứ giác OBKC có
OB//KC
OC//BK
góc BOC=90 độ
Do đó: OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
nên OK=BC
=>OK=AB
27 tháng 12 2022
THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
CW
27 tháng 11 2016
Đây chỉ là hướng giải, ko phải bài giải nhé ^^!
a) Chứng minh theo dấu hiệu hình hình hành có 1 góc vuông là hcn
b) Cm theo DH Tứ giác có 2 cạnh đối song song và bằng nhau là hình bình hành => AB = OI (2 cạnh đối)
c) Để OBIC là hình vuông thì OB = OC hay BD = AC <=> ABCD là hình vuông
CM
31 tháng 5 2017
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
a: Xét tứ giác IBKC có
IB//KC
IC//BK
Do đó: IBKC là hình bình hành
mà \(\widehat{BIC}=90^0\)
nên IBKC là hình chữ nhật