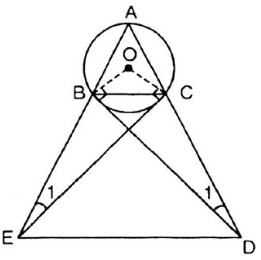
cho tam giác ABC nội tiếp đường tròn (O), xy là tiếp tuyến tại A của đường tròn. Một đường thẳng song song với xy cắt các cạnh AB, AC lần lượt tại D và E. chứng minh tứ giác BDEC là tứ giác nội tiép
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


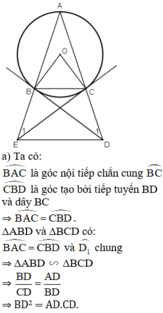
b) ΔABC cân tại A
⇒ AB = AC
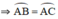
 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
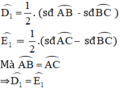
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
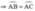
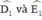 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
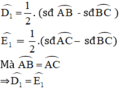
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

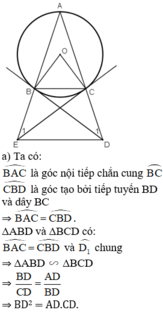
a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp

â ) Xét tứ giác BMNC , ta có :
goc BMC = 90o ( gt)
goc BNC = 90o ( gt )
goc BMC = goc BNC = 90o
Vay :tứ giác BMNC nội tiếp ( vì có 2 định M , N cùng nhìn BC dưới một góc 90o )
b) Tứ giác ANHM có : góc ANH = 900 ; góc HMA = 900 (giả thiết)
=> góc ANH + góc HMA = 90 + 90 = 1800
=> Tứ giác ANHM nội tiếp
=> góc AMN = góc ACB (góc ngoài tứ giác nội típ = đối góc trong)
Ta có: góc xAB = góc ACB (nội típ chắn cung AB)
=> góc AMN = góc xAB mà 2 góc ở vị trí so le trong
=> MN // xy
( Hình có bạn vẽ rồi nên mình giải câu b) thui ^^ )

Ai trả lời hộ điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinhanh lênnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn