cho hàm số y = f(x) = (-1/2) x
tìm x biết rằng f(x) = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2021
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
CM
27 tháng 12 2019
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
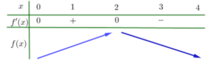
Từ bảng biến thiên, ta có nhận xét sau: 
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
CM
9 tháng 9 2018
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
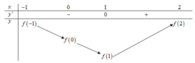
Nhận thấy
Để tìm 
ta so sánh f(-1) và f(2)
Theo giả thiết, 
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 
CM
17 tháng 4 2017
Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
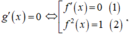
Từ bảng biến thiên, ta có:
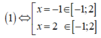
Và 
nên f(x) đồng biến trên [-1;2]
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có 
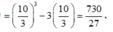
Vậy 
PT
1
20 tháng 7 2021
Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)
DD
Đoàn Đức Hà
Giáo viên
24 tháng 7 2021
\(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\)
Thế \(x=2\)ta được:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\)
Thế \(x=\frac{1}{2}\)ta được:
\(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\)
Ta có hệ phương trình:
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}f\left(2\right)=-\frac{13}{32}\\f\left(\frac{1}{2}\right)=\frac{47}{32}\end{cases}}\)
f(x)=2
=>-1/2x=2
hay x=-4