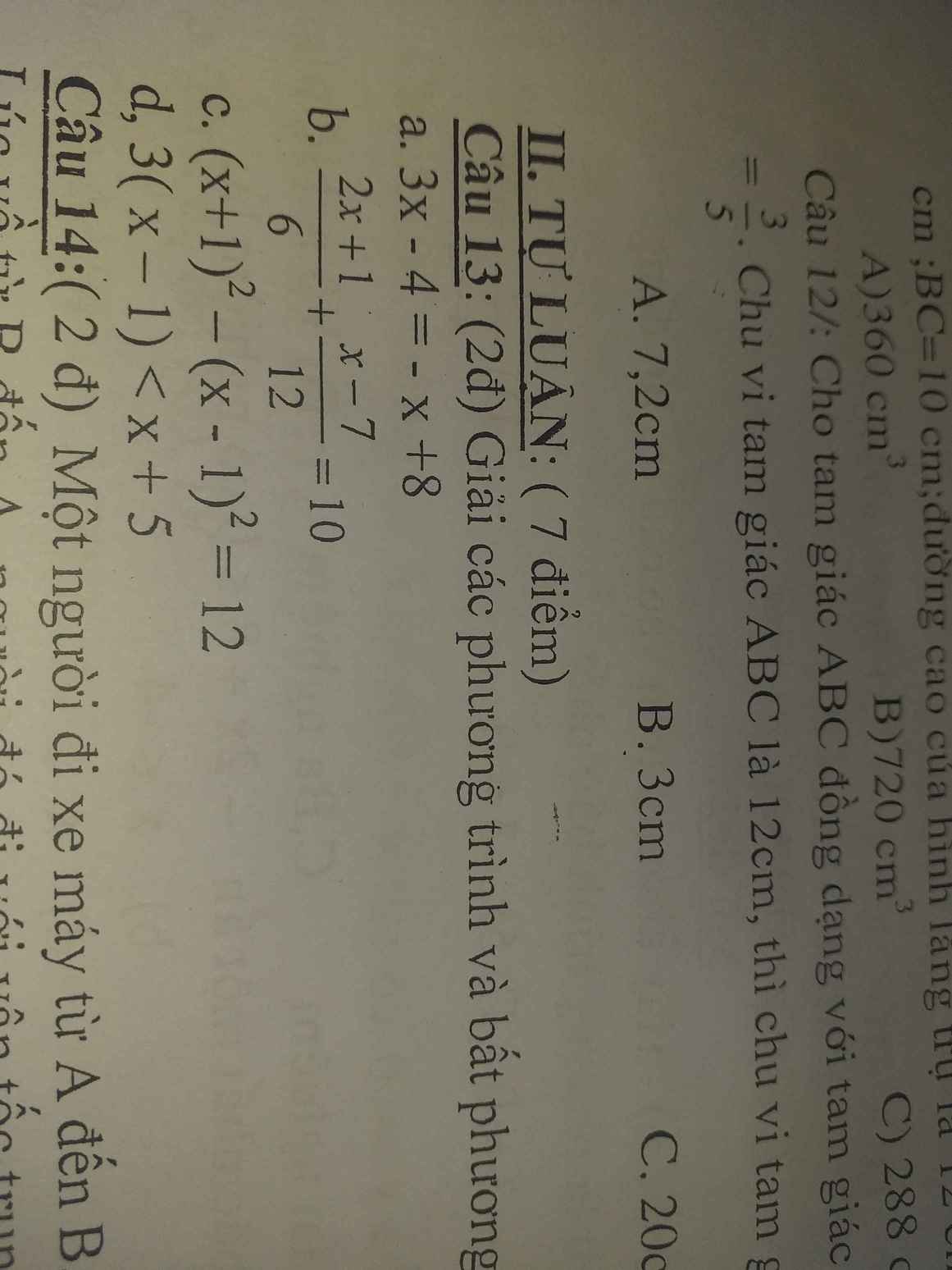Giúp mk vs mk đang cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2021
a: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{DAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔADM=ΔCBN
Suy ra: DM=BN
13 tháng 8 2021
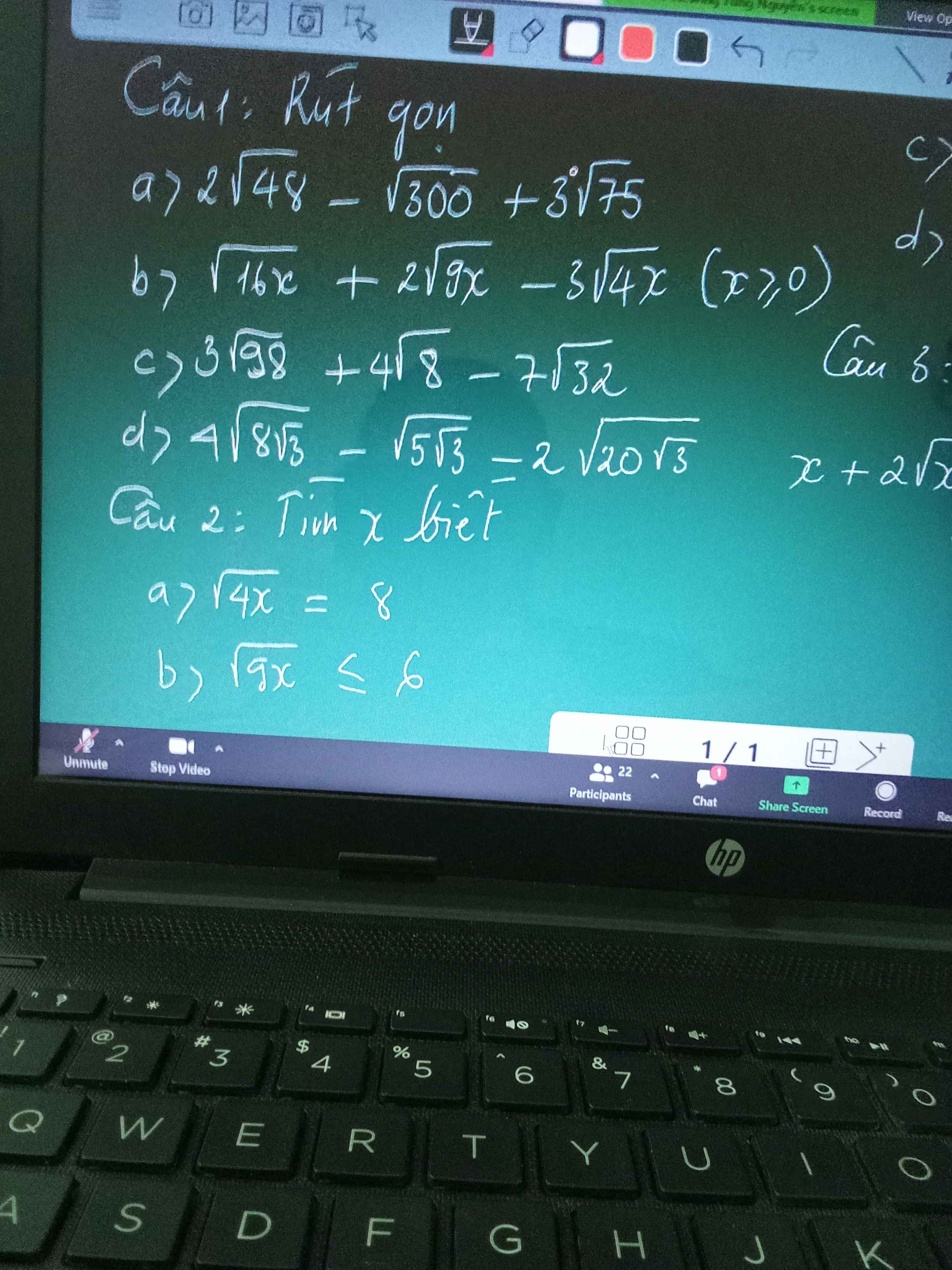
Câu 1
a)=\(8\sqrt{3}-10\sqrt{3}+15\sqrt{3}=13\sqrt{3}\)
b)=\(4\sqrt{x}+6\sqrt{x}-6\sqrt{x}=4\sqrt{x}\)
c)=\(21\sqrt{2}+8\sqrt{2}-28\sqrt{2}=\sqrt{2}\)
d)\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-\sqrt{5\sqrt{3}}-4\sqrt{5\sqrt{3}}\)
\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-5\sqrt{5\sqrt{3}}\)
câu 2
a)\(\Rightarrow4x=64\)\(\Rightarrow x=16\)
b)\(\Rightarrow9x\le36\)\(\Rightarrow x\le4\)
13 tháng 8 2021
Câu 2:
a: Ta có: \(\sqrt{4x}=8\)
\(\Leftrightarrow4x=64\)
hay x=16
b: Ta có: \(\sqrt{9x}\le6\)
\(\Leftrightarrow9x\le36\)
\(\Leftrightarrow x\le4\)
Kết hợp ĐKXĐ, ta được: \(0\le x\le4\)
PL
1
9 tháng 2 2022
a: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7\cdot b^2k^2+3\cdot bk\cdot b}{11\cdot b^2k^2-8\cdot b^2}=\dfrac{b^2k\left(7k+3\right)}{b^2\left(11k^2-8\right)}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7\cdot d^2k^2+3\cdot dk\cdot d}{11\cdot d^2k^2-8d^2}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
Do đó: \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
c: \(\dfrac{3a+2c}{3b+2d}=\dfrac{3bk+2dk}{3b+2d}=k\)
\(\dfrac{a}{b}=\dfrac{bk}{b}=k\)
Do đó: \(\dfrac{a}{b}=\dfrac{3a+2c}{3b+2d}\)
3 tháng 5 2021
Em cần giúp câu nào hả em? Em nên chụp 1-2 ý cho 1 lần hỏi nhá, như thế mọi người sẽ dễ dàng giúp em hơn
PN
12 tháng 5 2021
13
a, \(3x-4=-x+8\)
\(< =>3x+x=8+4\)
\(< =>4x=12\)
\(< =>x=\frac{12}{4}=3\)
b, \(\frac{2x+1}{6}+\frac{x-7}{12}=10\)
\(< =>\frac{2\left(2x+1\right)}{12}+\frac{x-7}{12}=\frac{120}{12}\)
\(< =>4x+2+x-7=120\)
\(< =>5x=120+5=125\)
\(< =>x=\frac{125}{5}=\frac{5^3}{5}=5^2=25\)
