Giúp mk bài này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
\(a,f\left(-\dfrac{1}{2}\right)=\left(-\dfrac{1}{2}\right)^2+4=\dfrac{1}{4}+4=\dfrac{17}{4}\\ f\left(5\right)=5^2+4=25+4=29\\ b,f\left(x\right)=10\Rightarrow x^2+4=10\Rightarrow x^2=6\Rightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\)
4 tháng 1 2022
a: f(-1/2)=1/4+4=17/4
f(5)=25+4=29
b: f(x)=10
nên \(x^2=6\)
hay \(x\in\left\{\sqrt{6};-\sqrt{6}\right\}\)
14 tháng 4 2022
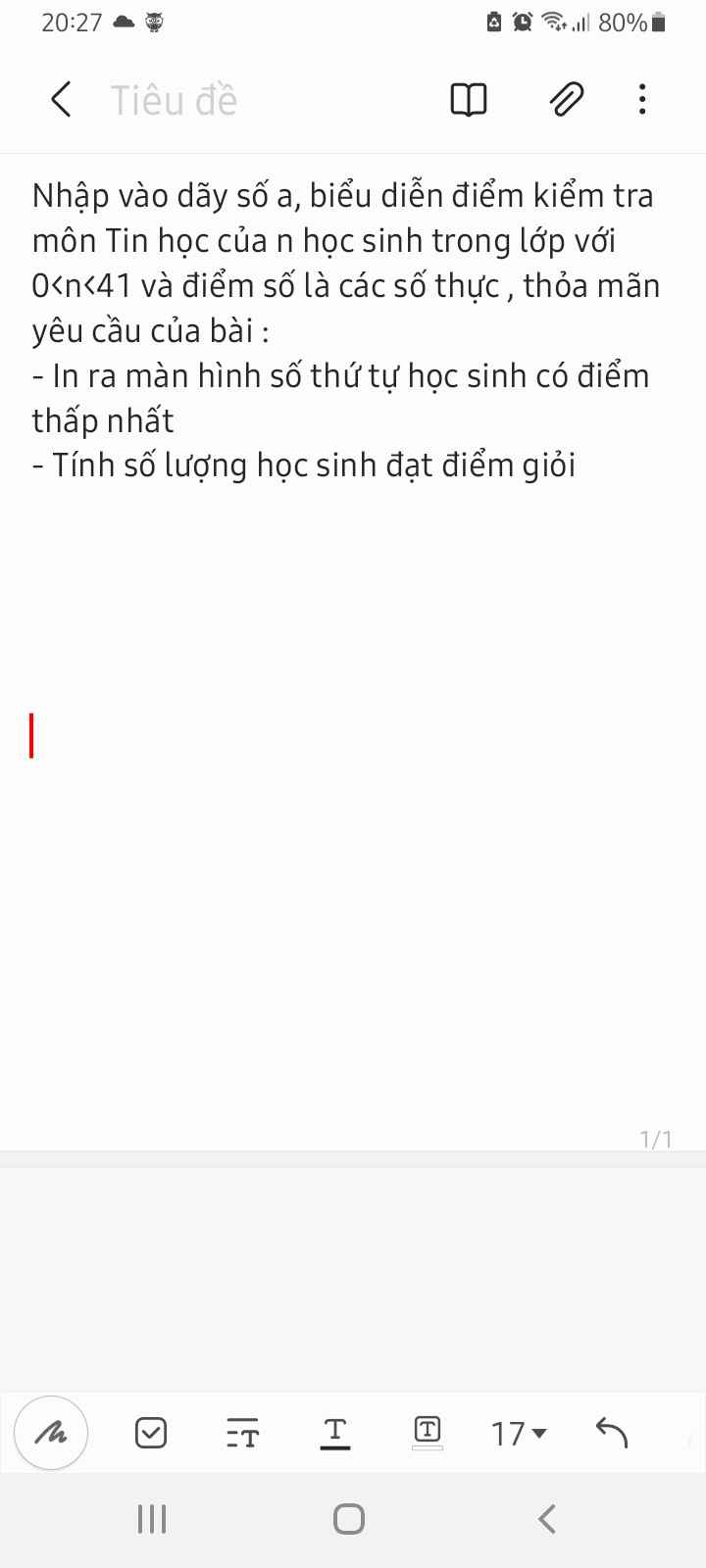
uses crt;
var a:array[1..42] of real;
i,n,dem:integer;
nn:real;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
nn:=a[1];
for i:=1 to n do
if nn>a[i] then nn:=a[i];
for i:=1 to n do
if nn=a[i] then write(i:4);
writeln;
dem:=0;
for i:=1 to n do
if a[i]>=8 then inc(dem);
writeln(dem);
readln;
end.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
b.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 2\\x>\dfrac{9}{2}\end{matrix}\right.\\-\dfrac{1}{3}< x< 7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}< x< 2\\\dfrac{9}{2}< x< 7\end{matrix}\right.\)
Hay \(S=\left(-\dfrac{1}{3};2\right);\left(\dfrac{9}{2};7\right)\)
d.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-\dfrac{11}{5}\\x\ge7\end{matrix}\right.\\-\dfrac{1}{2}< x< 3\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\) hay BPT vô nghiệm
29 tháng 8 2021
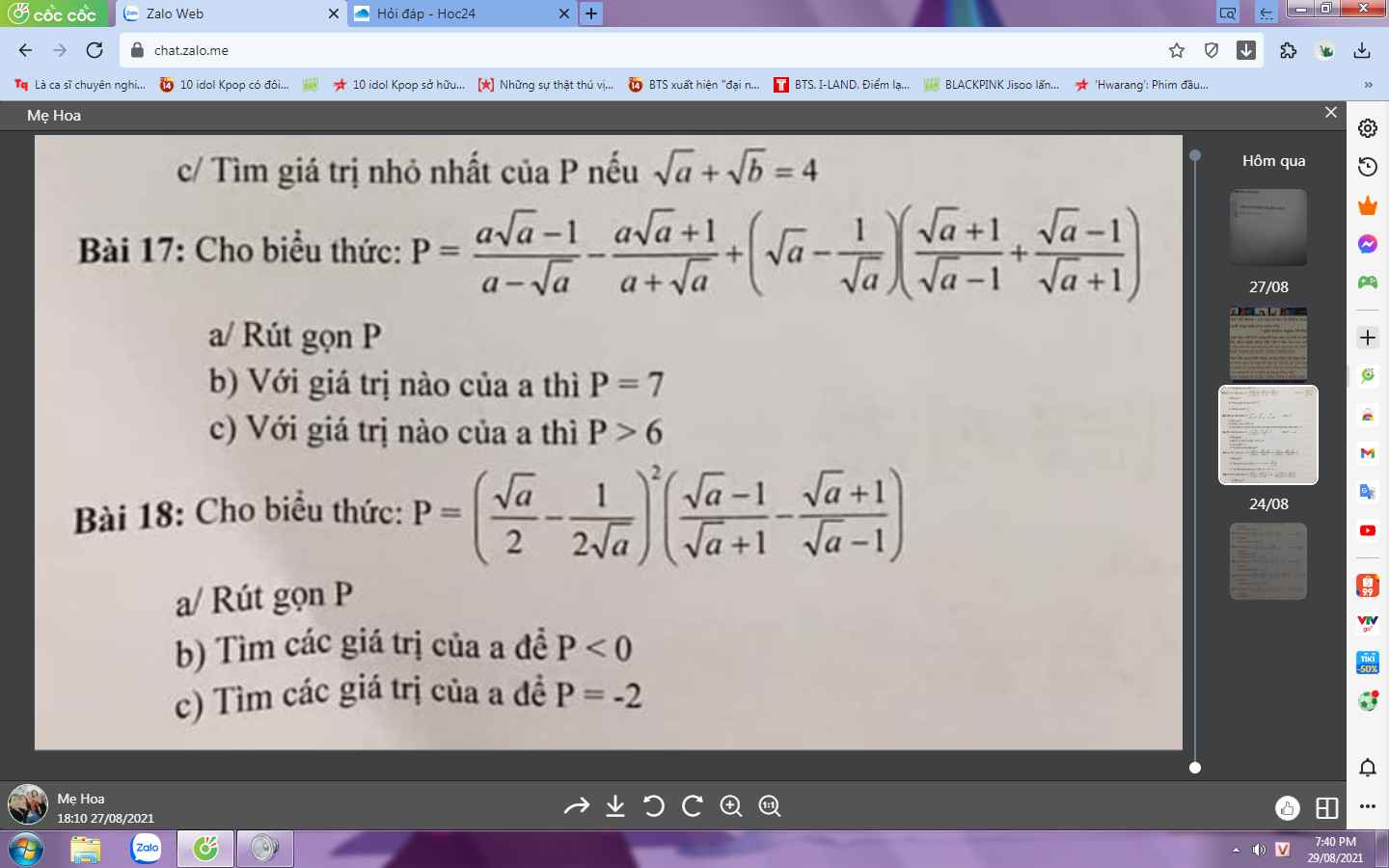
Bài 18:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(a-1\right)\cdot\left(-4\right)\cdot\sqrt{a}}{4a}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
b: Để P<0 thì -a+1<0
\(\Leftrightarrow-a< -1\)
hay a>1
c: Để P=-2 thì \(-a+1=-2\sqrt{a}\)
\(\Leftrightarrow-a+1+2\sqrt{a}=0\)
\(\Leftrightarrow a-2\sqrt{a}+1=2\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=2\)
\(\Leftrightarrow\sqrt{a}-1=\sqrt{2}\)
hay \(a=3+2\sqrt{2}\)
29 tháng 8 2021
Bài 17:
a: Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{2a+2}{\sqrt{a}}\)
\(=\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)
11 tháng 7 2021
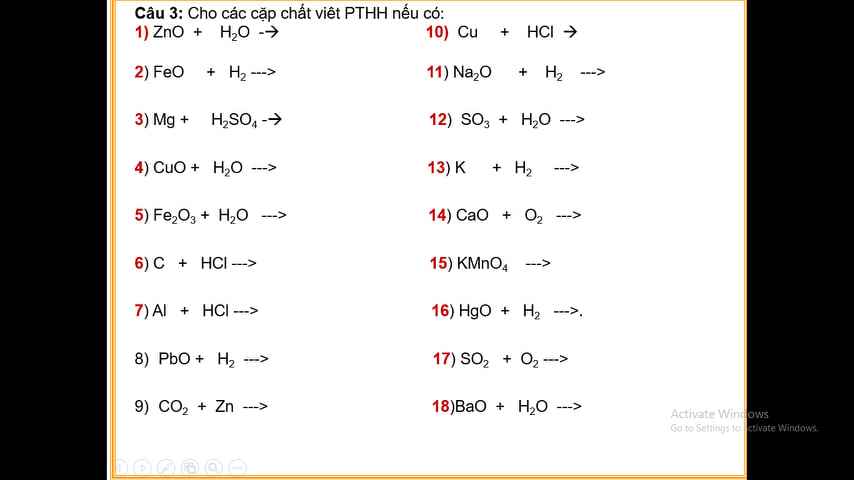
Câu 3 :
1) ZnO + H2O \(\rightarrow\)
2) FeO + H2 → Fe + H2O
3) Mg + H2SO4 → MgSO4 + H2
4) CuO + H2O →
5) Fe2O3 + 3H2O \(\rightarrow\) 2Fe(OH)3
6) C + HCl \(\rightarrow\)
7) 2Al + 6HCl → 2AlCl3 + 3H2
8) PbO + H2 → Pb + H2O
9) CO2 + Zn →
10) Cu + HCl →
11) Na2O + H2 \(\rightarrow\)
12) SO3 + H2O → H2SO4
13) 2K + H2 → 2KH
14) CaO + O2 →
15 ) 2KMnO4 \(\rightarrow\) K2MnO4 + MnO2 + O2
16) HgO + H2 → Hg + H2O
17) 2SO2 + O2 → 2SO3
18) BaO + H2O → Ba(OH)2
Chúc bạn học tốt
11 tháng 7 2021
Câu 2 : Công thức hóa học :
Mg (II) và O (II)
⇒ CTHH : MgO : magie oxit
H (I) và O (II)
⇒ CTHH : H2O : nước
C (II) và O (II)
⇒ CTHH : CO2 : khí cacbonic
Chúc bạn học tốt
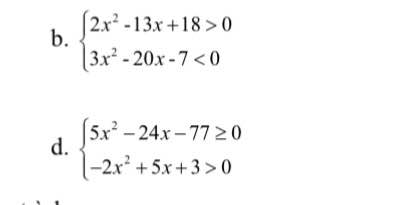
a: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
b: Xét ΔMHC vuông tại M và ΔNHC vuông tại N có
HC chung
\(\widehat{MCH}=\widehat{NCH}\)
Do đó: ΔMHC=ΔNHC
Suy ra: \(\widehat{MHC}=\widehat{NHC}\)
hay HC là tia phân giác của góc MHN
c: Xét ΔMHN có HM=HN
nên ΔHMN cân tại H
mà HC là đường phân giác
nên HC là đường trung trực
Mk cảm ơn ạ