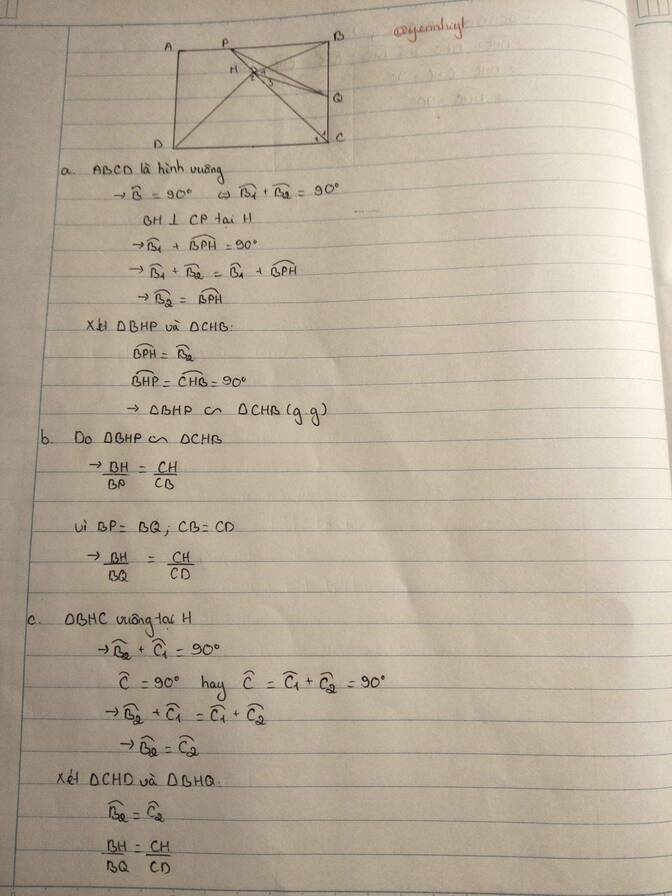Cho hình vuông ABCD. Trên cạnh AB, BC lấy lần lượt 2 điểm P và Q sao cho BQ=BP. H là hình chiếu của B trên cạnh CP. Chứng minh góc DQH = 90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2019
a) Xét tam giác BHP và tam giác CHB có: \(\widehat{HPB}=\widehat{HBC}\)( cùng phụ góc PBH) (1)
và \(\widehat{PHB}=\widehat{BHC}\left(=90^o\right)\)
=> tam giác BHP ~ tam giác CHB
=> \(\frac{BH}{HC}=\frac{BP}{BC}\Leftrightarrow\frac{BH}{HC}=\frac{BQ}{DC}\)( vì BP=BQ, BC=DC)
Ta lại có : \(\widehat{HPB}=\widehat{HCD}\) ( so le trong) (2)
Từ (1) , (2) => \(\widehat{HBC}=\widehat{HCD}\) => \(\widehat{HBQ}=\widehat{HCD}\)
Xét tam giác HBQ và tam giác HCD có:
\(\frac{BH}{HC}=\frac{BQ}{DC}\); \(\widehat{HBQ}=\widehat{HCD}\)
=> tam giác HBQ ~tam giác HCD
b) Có: tam giác HBQ ~tam giác HCD ( theo a)
=> \(\widehat{DHC}=\widehat{QHB}\)
mà \(\widehat{QHB}+\widehat{QHC}=\widehat{BHC}=90^o\)
=> \(\widehat{DHC}+\widehat{QHC}=\widehat{DHQ}=90^o\)
10 tháng 11 2019
Cho hình vuông ABCD . Trên cạnh BA và BC lấy hai điểm P và Q sao cho BP = BQ . Kẻ BH vuông góc với PC . CM :
a) Tam giác BHP đồng dạng với tam giác CHB
b) BH/BQ=CH/CD
c) Tam giác DHC đồng dạng với tam giác QHB
d) Góc DHQ = 90O
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)
