cho tam giác ABC, điểm D nằm giữa B và C. chứng minh AD nhỏ hơn nữa chu vi tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 9 2018
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
18 tháng 5 2022
XétΔABD có AD<AB+BD(1)
Xét ΔACD có AD<AC+CD(2)
Từ (1) và (2) suy ra \(2AD< AB+AC+BC\)
hay \(AD< \dfrac{AB+AC+BC}{2}=\dfrac{C_{ABC}}{2}\)
9 tháng 3 2019
Bài 1 :
Vì tam giác đó cân
=>
- Có 2 cạnh là 4m
- Có 2 cạnh là 9m
Mà theo bất đẳng thức tam giác , độ dài 1 cạnh bao nhờ cũng nhỏ hơn tổng độ dài 2 cạnh còn lại
=> Tam giác đó có 2 cạnh bằng 9m .
Chu vi tam giác đó là :
9 + 9 + 4 = 22 ( m)
Đáp số : 22m
NT
1
5 tháng 5 2017
theo BĐT trong tam giác ta có :
AB+BM>MA ( tg AMB)
AC+MC>MA (tg AMC)
cộng lạ nhé AB+AC+MC+MB> 2MA
AB+AC+BC> 2MA
<=> 2p > 2MA ( p là nữa chu vi )
=> p >MA (đpcm)
CM
12 tháng 5 2019
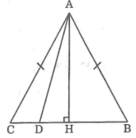
Kẻ AH ⊥ BC.
* Trường hợp H trùng với D
Ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
* Trường hợp H không trùng với D
Giả sử D nằm giữa H và C.
Ta có: HD < HC
Suy ra: AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.
19 tháng 7 2017
Kẻ \(AH\perp BC\)
- Nếu D trùng H thì \(AD< AC\) vì \(AH< AC\) ( đường vuông góc nhỏ hơn đường xiên )
- Nếu D không trùng H, giả sử D nằm giữa H và C. Ta có: \(HD< HC\)
\(\Rightarrow AD< AC\) ( hình chiếu nhỏ hơn thì đường xiên nhỏ hơn )
Vậy AD nhỏ hơn cạnh bên của \(\Delta ABC\)
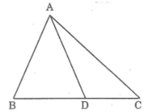
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .