không dùng máy tính chứng tỏ rằng 215216217.218219220 có 17 chữ số. giúp minh với thank you
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I
3
2 tháng 7 2016
vì tổng các chữ ssó là 1 nên hàng trăm là 1 và hàng chục và đơn vị là 0
số đó là 100.
số chia hết cho 2,5 có tận cùng là 0 hoặc 5 nên 100 chia hết cho 2.5
TT
15 tháng 10 2015
3 số tự nhiên liên tiếp sẽ có dạng a;a+1 và a+2
Tổng của 3 số là:a+a+1+a+2=3*a +3=3*(a+1) (chia hết cho 3)
Các số có 3 chữ số bắt đầu từ 100,kết thúc là số 999
=>Số số có 3 chữ số là: (999-100):1 +1=900 số
NM
1
.
.
.
12 tháng 10 2021
\(x^2+4y^2+z^2-2x+8y-6x+15=0\)
<=> \(\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1=0\)
mà \(\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2\)≥0
=> \(\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1\)≥1
=> ko có giá trị nào của x,y,z thỏa mãn
12 tháng 10 2021
\(A=\dfrac{1}{x^2-4x+9}=\dfrac{1}{\left(x-2\right)^2+5}\)
mà (x+2)2≥0
=> (x+2)2+5≥5
=> \(\dfrac{1}{\left(x-2\right)^2+5}\)≤ 1/5
=> Max A = 1/5 dấu ''='' xảy ra khi x=2
NT
1
H9
HT.Phong (9A5)
CTVHS
29 tháng 6 2023
\(\sqrt{2}\left(\sqrt{3}+1\right)\)
\(=\sqrt{6}+\sqrt{2}\)
Ta có: \(\left(\sqrt{6}+\sqrt{2}\right)^2=8+4\sqrt{3}\)
Và: \(\left(\sqrt{3}+2\right)^2=7+4\sqrt{3}\)
Ta thấy: \(8+4\sqrt{3}>7+4\sqrt{3}\)
Hay: \(\sqrt{2}\left(\sqrt{3}+1\right)>\sqrt{3}+2\) (đpcm)
NT
1
28 tháng 6 2021
CM bđt theo phương pháp tương đương:
Ta có: \(\sqrt{14}-\sqrt{13}< 2\sqrt{3}-\sqrt{11}\)
<=> \(\sqrt{14}+\sqrt{11}< \sqrt{12}+\sqrt{13}\)
<=> \(14+11+2\sqrt{14.11}< 12+13+2\sqrt{12.13}\)
<=> \(\sqrt{14.11}< \sqrt{12.13}\)
<=> \(14.11< 12.13\)
Ta có: 14.11 = 12.11 + 2.11 = 12.13 - 2.12 + 2.11 = 12.13 - 2(12 - 11) = 12.13 - 2 < 12.13
=> 14.11 < 12.13 (luôn đúng)
=> \(\sqrt{14}-\sqrt{13}< 2\sqrt{3}-\sqrt{11}\)(luôn đúng)
=????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
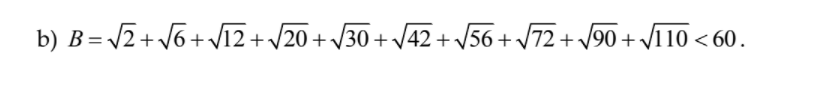