Trong một hộp đựng 7 bi xanh, 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên 3 viên bi, tính xác suất để lấy được không quá 2 bi đỏ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Trường hợp 1: Lấy 3 viên bi cùng màu xanh ⇒ có 
cách chọn Trường hợp 2: Lấy 3 viên bi cùng màu đỏ ⇒ có 
cách chọn Trường hợp 3: Lấy 3 viên bi cùng màu vàng ⇒ có 
cách chọn Do đó suy ra 
.
CM
11 tháng 11 2019
Lấy ngẫu nhiên một hộp trong 3 hộp nên xác suất là 1 3
TH1. Lấy được hộp A và lấy 1 bi xanh trong hộp A, ta được xác suất là P A = 3 8
TH2. Lấy được hộp B và lấy 1 bi xanh trong hộp B, ta được xác suất là P B = 3 5
Vậy xác suất cần tính là
P = 1 3 P A + P B = 1 3 3 8 + 3 5 = 13 40
Đáp án cần chọn là D
CM
4 tháng 10 2017
Đáp án D
Lấy ngẫu nhiên một hộp trong 3 hộp nên xác suất là 1 3 .
TH1. Lấy được hộp A và lấy 1 bi xanh trong hộp A
ta được xác suất là P A = 3 8 .
TH2. Lấy được hộp B và lấy 1 bi xanh trong hộp B
ta được xác suất là P B = 3 5
Vậy xác suất cần tính là
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
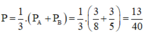
Không gian mẫu: \(C_{15}^4\)
a.
Số cách lấy 4 viên bi trong đó có 3 viên màu đỏ: \(C_7^3C_8^1\)
Xác suất: \(P=\dfrac{C_7^3.C_8^1}{C_{15}^4}\)
b.
Lấy 4 viên không có viên đỏ nào (lấy từ 8 viên 2 màu còn lại): \(C_8^4\) cách
Lấy 4 viên có ít nhất 1 viên đỏ: \(C_{15}^4-C_8^4\)
Xác suất: \(P=\dfrac{C_{15}^4-C_8^4}{C_{15}^4}\)
c.
Các trường hợp thỏa mãn: (2 đỏ 1 xanh 1 vàng), (1 đỏ 2 xanh 1 vàng), (1 đỏ 1 vàng 2 xanh)
Số cách lấy: \(C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2\)
Xác suất: \(P=\dfrac{C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2}{C_{15}^4}\)
CM
8 tháng 2 2017
Gọi A là biến cố lấy ra được 3 viên bi màu đỏ.
Số cách lấy 3 viên bi từ 20 viên bi là C 20 3 nên ta có Ω = C 20 3 = 1140 .
Số cách lấy 3 viên bi màu đỏ là C 8 3 = 56 nên Ω A = 56 .
Do đó: P ( A ) = 56 1140 = 14 285
Đáp án B
CM
26 tháng 5 2019
Đáp án B
Có các cách chọn sau:
+) 1 bi đỏ, 1 bi vàng, 3 bi xanh, suy ra có C 6 1 C 7 1 C 5 3 = 420 cách.
+) 2 bi đỏ, 2 bi vàng, 1 bi xanh, suy ra có C 6 2 C 7 2 C 5 1 = 1575 cách.
Suy ra xác suất bằng 420 + 1575 C 18 5 = 95 408 .
Không gian mẫu: \(C_{15}^3\)
Số cách lấy nhiều hơn 2 bi đỏ (nghĩa là cả 3 viên đều đỏ): \(C_5^3\)
Số cách lấy không quá 2 bi đỏ: \(C_{15}^3-C_5^3\)
Xác suất: \(\dfrac{C_{15}^3-C_5^3}{C_{15}^3}=\dfrac{89}{91}\)