cho tam giác vuông abc, <a=90 độ có <b=anpha.trên ac lấy e sao cho<eba=1/3.anpha. trên tia đối của eb lấy điểm d sao cho ed=bc. chứng minh tam giác ced cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)

\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)

https://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.htmlhttps://olm.vn/hoi-dap/detail/239868952049.html

Câu 17: Cho ABC có AB = AC và = 2 có dạng đặc biệt nào:
A. Tam giác cân B. Tam giác đều
C. Tam giác vuông D. Tam giác vuông cân
Câu 18: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Độ dài cạnh BC là:
A. 7cm B. 12,5cm C. 5cm D.
Câu 19: Tam giác ABC có AB = 12cm, AC = 13cm, BC = 5cm. Khi đó vuông tại:
A. Đỉnh A B. Đỉnh B C. Đỉnh C D. Tất cả đều sai
Câu 20: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Khẳng định nào sau đây sai?
A. ABM = ACM B. ABM= AMC
C. AMB= AMC= 900 D. AM là tia phân giác CBA
Câu 22: Cho ABC= DEF. Khi đó: .
A. BC = DF B. AC = DF
C. AB = DF D. góc A = góc E
Câu 23. Cho PQR= DEF, DF =5cm. Khi đó:
A. PQ =5cm B. QR= 5cm C. PR= 5cm D.FE= 5cm

Xét ΔABC và ΔHAC có:
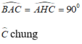
Suy ra: ΔABC đồng dạng với ΔHAC ( g.g)
Chọn đáp án A

xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BC^2+AB^2\)
\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Vậy: \(AB=4\sqrt{5}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:
\(MP^2=MN^2+NP^2\)
\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)
hay MN=4cm
Vậy: MN=4cm
Bài 1 :
- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)
\(\Leftrightarrow AB^2+8^2=12^2\)
\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )
Vậy ...
Bài 2 :
- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :
\(MN^2+NP^2=MP^2\)
\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)
\(\Leftrightarrow MN=4\) ( đvđd )
Vậy ...