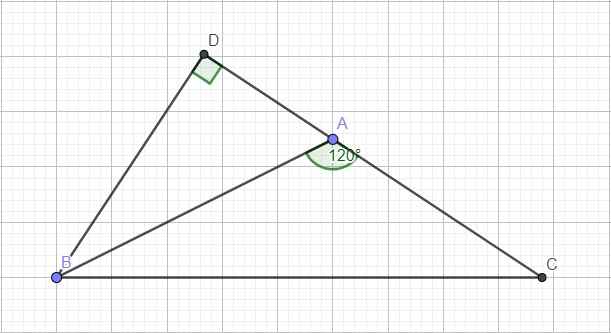
cho tam giác ABC có B=120,BC=c,AC=b.tinh BC theo b,c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
EC
0
NP
1
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
K
0
29 tháng 8 2015
Kẻ CE vuông góc với AB, ta có ngay tam giác ACE vuông có một góc nhọn 60. Suy ra \(AE=\frac{1}{2}AC=\frac{b}{2},CE=\frac{\sqrt{3}}{2}b\). Xét tam giác vuông EBC có '\(EB=c+\frac{b}{2},EC=\frac{\sqrt{3}}{2}b\to a^2=BC^2=BE^2+CE^2=\left(c+\frac{b}{2}\right)^2+\left(\frac{\sqrt{3}}{2}b\right)^2=c^2+bc+b^2\)
P
1
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 8 2018
.png)
Chu vi tam giác ABC bằng: 5 + 6 + 8 = 19 (cm)
Dễ dàng thấy ngay \(\Delta ABE=\Delta BAC\left(g-c-g\right)\)
Vậy nên \(P_{ABE}=P_{BAC}=19cm.\)
Ta thấy \(\Delta BCD=\Delta CBA\left(g-c-g\right)\)
Vậy nên \(P_{BCD}=P_{CBA}=19cm.\)
Ta thấy \(\Delta ACF=\Delta CAB\left(g-c-g\right)\)
Vậy nên \(P_{ACF}=P_{CBA}=19cm.\)
\(P_{DEF}=DE+EF+FD=2.8+2.6+2.5=38cm.\)
NL
0
TN
0
minhf vt goiwj ys hoy
bạn dùng công thức trong tam giác thường:
b2 = a2 + c2 - 2.ac.cosB (tức là AC2 = BC2 + AB2 - 2.AB,BC.cosB)
tính đc AC = x
trên tia BC, vẽ BE=BA sao cho E&C nằm khác phía so với B. dễ dang chứng minh dc tam giác ABE là tam giác đều. Hạ AH vuông góc với BE
=> AH=AB.sin60
tính dc AH=y
Trong tam giác AHC có AC=x, AH=y
=> sinC=AH/AC
=>trị số góc C
=>góc BDC = 180 - (gócC + 60) (trong tam giác BCD ý) =>sin(BDC)
dùng định lý hàm số sin
=> BD = BC*(sinC/sinBDC)
Áp dụng định lý hàm số COS ta có:
AC^2 = AB^2+AC^2 - 2AB.AC.cosB
= 12^2 + 6^2 -2.12.6.(-1/2) = 252 ------> AC = CĂN 252
Vì BD là phân giác của góc B nên theo tính chất ta có:
AD/AC =AB/BC = 6/12 = 1/2
----> DC = 2 AD , mà AC = CĂN 252 ------> AD= 1/3 căn 252
Áp dụng định lý hàm số COS đồi với tam giác ABD có:
AD^2=AB^2+BD^2 - 2AB.BD.cosB
<=>(1/3 căn 252)^2= 6^2+ BD^2 - 2.6.BD.(1/2)
<=> BD^2 - 6BD + 8 =0
<=> BD = 4 hoặc BD =2
Vậy: BD = 4 (cm)
Trên đây là bài giải với ĐK: BD là phân giác trong.
còn nếu BD là phân giác ngoài thì tỉ lệ: AC/AD =AB/BC
DO VẬY BD = 8 cm