Cho tam giác ABC có BC= 6cm, đường cao AH= 4cm.
a/ Tính diện tích tam giác ABC.
b/ Cắt tam giác ABC thành ba mảnh ghép lại thành một hình chữ nhật. Tính diện tích của mỗi mảnh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
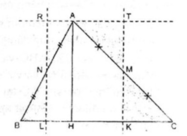
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC

1. Diện tích tam giác ABC là:
\(\dfrac{1}{2}.45.28=630\) cm vuông
2. Bạn có chép sai đề bài không tại chia ra nó lẻ lắm

Câu 1 :
Nửa chu vi hình chữ nhật là :
92 : 2 = 46 ( m )
Nếu tăng chiều rộng 5 m và giảm chiều dài 5 m thì mảnh vườn trở thành hình vuông . Vậy lúc đầu chiều dài hơn chiều rộng : 5 x 2 = 10 ( m )
Chiều dài mảnh vườn hình chữ nhật là ;
( 46 + 10 ) : 2 = 28 ( m )
Chiều rộng mảnh vườn hình chữ nhật là :
46 - 28 = 18 ( m )
Diện tích mảnh vườn là :
18 x 28 = 504 ( m2)
Đáp số : 504 m2
Câu 2 :
a) Chiều cao hình tam giác ABC là :
30 x 2/3 = 20 ( cm )
Diện tích tam giác ABC là :
30 x 20 : 2 = 300 ( cm2)
b) Diện tích tam giác ACM là :
300 x 20 : 100 = 60 ( cm2)
Vì tam giác ACM có cùng chiều cao AH với tam giác ABC nên độ dài cạnh CM là :
60 x 2 : 20 = 6 ( cm )
Đáp số : a) 300 cm2
b) 6 cm

a/
\(S_{\Delta ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.6.4=12cm^2\)
b/
Gọi D và E lần lượt là trung điểm của AB và AC
Từ B dựng đường thẳng vuông góc BC cắt DE tại M
Từ C dựng đường thẳng vuông góc BC cắt DE tại N
Ta có
DA=DB; EA=EC => DE là đường trung bình của tg ABC => DE//BC => MN//BC
Ta có
\(BM\perp BC;CN\perp BC\)=> BM//CN (cùng vuông góc với BC)
=> BCNM là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hbh)
Mà \(\widehat{DBC}=90^o\)
=> BCNM là HCN (Hình bình hành có 1 góc vuông là HCN)
Ta có
Gọi I là giao của DE với AH ta có
DE//BC (cmt); \(AH\perp BC\Rightarrow AH\perp DE\)
DE//BC (cmt) \(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}=\frac{AI}{HI}=1\) => I là trung điểm của AH => IA=IH
Ta có
\(S_{\Delta ABC}=S_{BCED}+S_{\Delta ADI}+S_{AEI}\) (1)
\(S_{BCNM}=S_{BCED}+S_{\Delta BDM}+S_{\Delta CEN}\) (2)
Xét tg vuông ADI và tg vuông BDM có
DA=DB; \(\widehat{ADI}=\widehat{BDM}\) (góc đối đỉnh) => tg ADI = tg BDM (hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) (3)
C/m tương tự ta cũng có tg AEI = tg CEN (4)
Từ (1) (2) (3) (4) \(\Rightarrow S_{\Delta ABC}=S_{BCNM}\)
=> 3 mảnh cắt từ tg ABC là hình thang BCED; tg ADI và tg AEI
Ta có DE là đường trung bình của tg ABC => \(DE=\frac{BC}{2}=\frac{6}{2}=3cm\)
IA=IH (cmt) => IA=IH=4:2=2 cm
\(S_{BCED}=\frac{\left(BC+DE\right).IH}{2}=\frac{\left(6+3\right).2}{2}=9cm^2\)
\(S_{\Delta ADI}+S_{\Delta AEI}=S_{\Delta ADE}=\frac{1}{2}.DE.IA=\frac{1}{2}.3.2=3cm^2\)
Do tg ABC không có thêm điều kiện nào nên không thể tính riêng rẽ diện tích của hai tg ADI và AEI

Bạn xem lời giải của bài tương tự phía dưới nhé
Câu hỏi của nguyen yen nhi - Toán lớp 5 - Học toán với OnlineMath