Trong tam giác ABC, chứng minh rằng các trung điểm của các cạnh, các chân đường cao, các trung điểm của các đoạn nối từ trực tâm tới mỗi đỉnh cùng thuộc một đường tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2018
I, J, K lần lượt là chân đường cao hạ từ A, B, C; H là giao điểm ba đường cao
M, N, P lần lượt là trung điểm của BC , AC, AB
D, E, F lần lượt là trung điểm của HA, HB, HC
O là giao điểm của NE và PF
+) NP là đường trung bình tam giác ABC => NP//=1/2 BC (1)
EF là đường trung bình tam giác HCB => EF//=1/2 BC (2)
Từ (1), (2) => NFEP là hình bình hành (3)
NF là đường trung bình tam giác ACH => NF//AH=> NF//AI mà AI vuông BC , BC//EF => NF vuông EF (4)
Từ (3), (4) => NFEP là hình chữ nhật => Tâm đường tròn ngoại tiếp NFEP là O giao của FP và NE
và O là trung điểm FP, O là trung điểm NE
+) Tương tự NDEM là hình chữ nhật => Tâm đường tròn ngoại tiếp NDEM là O ( trung điểm NE)
=> O là trung điểm DM
+) Tam DIM vuông tại I => Tâm đường tròn ngoại tiếp DIM là O trung điểm DM
+) Tương tự O là tâm đường tròn ngoại tiếp tam giác FJP, EKN
=> Vậy 9 điểm trên cùng thuộc đường tròn tâm O đường kính NE
11 tháng 11 2018
Câu hỏi của Mavis Vermillion - Toán lớp 9 - Học toán với OnlineMath Em tham khảo ở link này nhé!
CM
19 tháng 5 2019
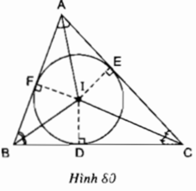
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
CM
1 tháng 11 2017
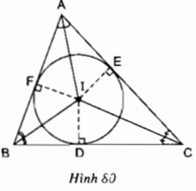
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
