Ba phân số đều có tử bằng 1 và tổng của ba phân số đó bằng 1. Hiệu của phân số thứ nhất và phân số thứ hai bằng phân số thứ ba, còn tổng của phân số thứ nhất và phân số thứ hai bằng
5 lần phần số thứ ba. Tìm các phân số đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2019
Gọi các phân số cần tìm là x, y, z.
Tổng của ba phân số bằng 1 nên:
x + y + z = 1 (1)
Hiệu của phân số thứ nhất và thứ hai bằng phân số thứ ba nên:
x - y = z (2)
Tổng của phân số thứ nhất và thứ hai bằng 5 lần phân số thứ ba nên:
x + y = 5z (3)
Từ (1), (2), (3) ta có hệ:
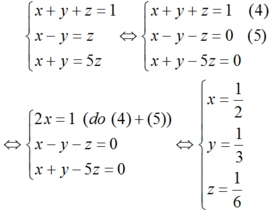
Vậy ba phân số cần tìm lần lượt là:
DM
30 tháng 3 2017
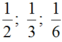
Gọi p/s thứ nhất là \(\dfrac{1}{x}\), p/s thứ 2 là \(\dfrac{1}{y}\), p/s thứ 3 là \(\dfrac{1}{z}\)
Theo đề bài ta có : \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\) (1)
và \(\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{z}\); \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\).
Thay biểu thức \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\) trên vào (1) ta được :
\(5\cdot\left(\dfrac{1}{z}\right)+\dfrac{1}{z}=1\Rightarrow z=6\) Vậy phân số thứ ba là \(\dfrac{1}{6}\).
Ta có : \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\dfrac{1}{6}\end{matrix}\right.\left(Đề-bài\right)\)
Bài toán tổng hiệu \(\dfrac{1}{x}\) là số lớn, \(\dfrac{1}{y}\) là số bé (do \(\dfrac{1}{x}-\dfrac{1}{y}\) ra số dương).
Vậy \(\dfrac{1}{x}=\dfrac{\left(\dfrac{1}{6}+5\cdot\dfrac{1}{6}\right)}{2}=\dfrac{1}{2}\); \(\dfrac{1}{y}=5\cdot\dfrac{1}{6}-\dfrac{1}{2}=\dfrac{1}{3}\)
Vậy phân số thứ nhất là \(\dfrac{1}{2}\), phân số thứ hai là \(\dfrac{1}{3}\), phân số thứ ba là \(\dfrac{1}{6}\).
14 tháng 3 2023
Gọi ba phân số đó là a/b, c/d và e/f. Ta có hệ phương trình sau: a/b + c/d = 31/24 (1) c/d + e/f = 7/8 (2) a/b + e/f = 11/12 (3) Giải hệ phương trình này bằng cách cộng (1) và (2), trừ (2) và (3), ta có: (a/b + c/d) + (c/d + e/f) = 31/24 + 7/8 a/b + e/f = 11/12 Suy ra: a/b = 3/8 c/d = 5/24 e/f = 1/4 Vậy ba phân số đó lần lượt là 3/8, 5/24 và 1/4.
1 tháng 3 2019
Gọi 3 phân số đó là a, b, c
Theo đề,
a+b=31/24
<=> a=(31/24)-b
<=> a=(31-24b)/24
b+c=7/8
<=> c=(7/8)-b
<=> c=(7-8b)/8
a+c=11/13
Thay a và c vào,
[(31-24b)/24] + [(7-8b)/8] = 11/13
[(31-24b)/24] + [(21-24b)/24] = 11/13
(52-48b)/24 = 11/13
13(52-48b) = (11)(24)
<=> 676 - 624b = 264
412 = 624b
b=(412/624)= 206/312 = 103/156
<=> c = (7/8) - (103/156)= 67/312
<=> a = (11/13) - (67/312) = 197/312
Đáp án:
phân số thứ nhất 197/312
phân số thứ hai 103/156
phân số thứ ba 67/312
1 tháng 3 2019
Gọi 3 phân số đó là a, b, c
Theo đề,
a+b=31/24
<=> a=(31/24)-b
<=> a=(31-24b)/24
b+c=7/8
<=> c=(7/8)-b
<=> c=(7-8b)/8
a+c=11/13
Thay a và c vào,
[(31-24b)/24] + [(7-8b)/8] = 11/13
[(31-24b)/24] + [(21-24b)/24] = 11/13
(52-48b)/24 = 11/13
13(52-48b) = (11)(24)
<=> 676 - 624b = 264
412 = 624b
b=(412/624)= 206/312 = 103/156
<=> c = (7/8) - (103/156)= 67/312
<=> a = (11/13) - (67/312) = 197/312
Đáp án:
phân số thứ nhất 197/312
phân số thứ hai 103/156
phân số thứ ba 67/312
15 tháng 3 2021
Tổng của ba phân số là:
\(\left(\dfrac{11}{15}+\dfrac{23}{20}+\dfrac{13}{12}\right):2=\dfrac{89}{60}\)
Phân số thứ nhất là:
\(\dfrac{89}{60}-\dfrac{23}{20}=\dfrac{20}{60}=\dfrac{1}{3}\)
Phân số thứ hai là:
\(\dfrac{89}{60}-\dfrac{13}{12}=\dfrac{89}{60}-\dfrac{65}{60}=\dfrac{24}{60}=\dfrac{2}{5}\)
Phân số thứ ba là:
\(\dfrac{89}{60}-\dfrac{1}{3}-\dfrac{2}{5}=\dfrac{89}{60}-\dfrac{20}{60}-\dfrac{24}{60}=\dfrac{45}{60}=\dfrac{3}{4}\)
BF
11 tháng 3 2023
Tổng của 3 phân số là:
`(11/15 + 23/20 + 13/12) : 2 = 89/60`
Phân số thứ nhất là:
`89/60 - 23/20 = 1/3`
Phân số thứ hai là:
`89/60 - 13/12 = 2/5`
Phân số thứ ba là:
`89/60 - 11/15 = 3/4`
20 tháng 3 2017
phân số 1 + phân số 2 = 31/24
Phân số 2 + phân số 3 = 7/8
Phân số 3 + phân số 1 = 11/12
Vậy (p1 + p2 + p3) . 2 = 31/24+7/8+11/12=37/12
p1+p2+p3=37/12:2=37/24
Phân số 3 là:
37/24-31/24=...
Phân số hai là:
37/24-11/12=...
Phân số ba là:
37/24-7/8=...
