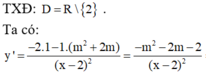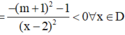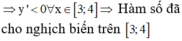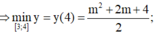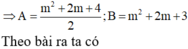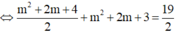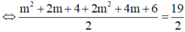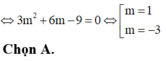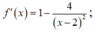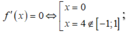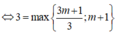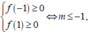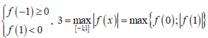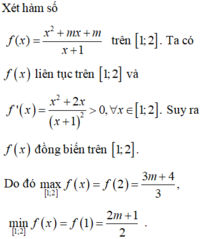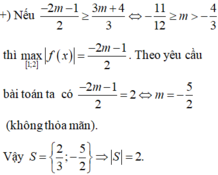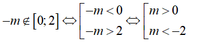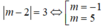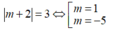câu 19: Tìm giá trị thực của tham số m khác 0 để hàm số y= mx^2-2mx-3m-2 có giá trị nhỏ nhất bằng -10 trên R
câu 20: Gọi S là tập hợp tất cả giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y=f(x)=4x^2-4mx+m^2-2m trên đoạn [-2;0] bằng 3 . Tính tổng T các phần tử của S