1 người đi xe máy trên đoạn đường đầu đi được 12km trong 20p, đoạn đường tiếp theo đi được 24km trong 35p a, tính Vtb trên mỗi quảng đường Giúp mk nhanh vs ạ, mk đang cần gấp, mà bn nào thấy đề tương tự như v thì cho mk xin câu b luôn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1: Tóm tắt
\(S_1=24km\)
\(V_1=12km\)/\(h\)
\(S_2=12km\)
\(V_2=45'=0,75h\)
_______________
a) \(t_1=?\)
b) \(V_{TB}\)
Giải
a) Thời gian người đó đạp xe trên quãng đường đầu là: \(t_1=\frac{S_1}{V_1}=\frac{24}{12}=2\left(h\right)\)
b) Ta có công thức tính vận tốc trung bình là: \(V=\frac{S_1+S_2+....+S_n}{t_1+t_2+t_3+....+t_n}\)
Vậy vận tốc trung bình của người đó trên quãng đường là:
\(V_{TB}=\frac{S_1+S_2}{t_1+t_2}=\frac{24+12}{2+0,75}\approx13\)(km/h)
Bài 2: Tóm tắt
\(S_1=600m=0,6km\)
\(t_1=2'=\frac{1}{30}\left(h\right)\)
\(S_2=10,8km\)
\(t_2=0,75h\)
_________________
a) \(V_1=?;V_2=?\)
b) \(S_{KC}=?\)
Giải
a) Vận tốc của người thứ nhất là: \(V_1=\frac{S_1}{t_1}=\frac{0,6}{\frac{1}{30}}=18\)(km/h)
Vận tốc của người thứ 2 là: \(V_2=\frac{S_2}{t_2}=\frac{10,8}{0,75}=14,4\) (km/h)
=> Người thứ nhất đi nhanh hơn người thứ 2.
b) Do đi cùng lúc => thời gian đi của 2 người là như nhau và vận tốc đã cho
=> Hai người cách nhau số km là: \(S-t\left(V_1+V_2\right)=S-\frac{1}{3}\left(18+14,4\right)=S-10,8\)
Theo đề thì còn cần phải dựa vào khoảng cách của 2 người khi 2 người bắt đầu đi nữa.
a) Thời gian người đó đạp xe trên quãng đường thứ nhất là :
24 : 12 = 2 (giờ)
b) Đổi : 45 phút = 0,75 giờ
=> Vận tốc trung bình của người đi xe đạp trên cả quãng đường là :
(S1 + S2) / (t1 + t2) = (12+24) / (2+0,75) = 13 (km/h)

xin lỗi hình như đề bạn còn thiếu vận tốc nửa quãng đường sau của phần đường còn lại
Bạn giải bài này theo hướng
Vận tốc trung bình của người đó trên cả quãng đường
\(v_{tb}=\dfrac{\dfrac{t}{2}\left(v_1+v_2\right)}{t}\Rightarrow\dfrac{1}{2}\left(40+v_2\right)=30\Rightarrow v_2=20\left(\dfrac{km}{h}\right)\)
vận tốc của người đó trên phần đường còn lại là
\(v_2=\dfrac{s}{\dfrac{s}{2}\left(v_3+?\right)}\Rightarrow20=\dfrac{1}{\dfrac{1}{2}\left(v_3+?\right)}\)

Giải:
Trong một phần ba đoạn đường đầu:
S 1 = v 1 . t 1 ⇒ t 1 = S 1 v 1 = S 3. v 1
Tương tự: t 2 = S 2 v 2 = S 3. v 2 ; t 3 = S 3 v 3 = S 3. v 3
Mà v t b = S t 1 + t 2 + t 3 = S S 3. v 1 + S 3. v 2 + S 3. v 3 = 1 1 3. v 1 + 1 3. v 2 + 1 3. v 3 = 36 , 62 k m / h

Thời gian đi trên 1/3 đoạn đường đầu là:
\(t_1=\dfrac{AB}{3v_1}=\dfrac{AB}{3.14}=\dfrac{AB}{42}\left(h\right)\)
Thời gian đi trên 1/3 đoạn đường tiếp theo là:
\(t_2=\dfrac{AB}{3v_2}=\dfrac{AB}{3.16}=\dfrac{AB}{48}\left(h\right)\)
Thời gian đi trên 1/3 đoạn đường cuối cùng là:
\(t_3=\dfrac{AB}{3v_3}=\dfrac{AB}{3.8}=\dfrac{AB}{24}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường là:
\(v_{tb}=\dfrac{AB}{t_1+t_2+t_3}=\dfrac{AB}{\dfrac{AB}{42}+\dfrac{AB}{48}+\dfrac{AB}{24}}=\dfrac{AB}{AB\left(\dfrac{1}{42}+\dfrac{1}{48}+\dfrac{1}{24}\right)}=\dfrac{1}{\dfrac{1}{42}+\dfrac{1}{48}+\dfrac{1}{24}}=\dfrac{336}{29}\left(km/h\right)\)
\(=>Vtb=\dfrac{S}{t1+t2+t3}=\dfrac{S}{\dfrac{\dfrac{1}{3}S}{v1}+\dfrac{\dfrac{1}{3}S}{v2}+\dfrac{\dfrac{1}{3}S}{v3}}\)
\(=>vtb=\dfrac{S}{\dfrac{S}{42}+\dfrac{S}{48}+\dfrac{S}{24}}=\dfrac{S}{\dfrac{S\left(48.24+42.24+48.42\right)}{48384}}=\dfrac{48384}{4176}=11,6km/h\)

a)Vận tốc xe trên đoạn đường 12km là: \(v_1=\dfrac{S_1}{t_1}=\dfrac{12}{\dfrac{21}{60}}=\dfrac{240}{7}km/h\)
Vận tốc xe trên quãng đường còn lại: \(v_2=\dfrac{S_2}{t_2}=\dfrac{30-12}{\dfrac{30}{60}}=36km/h\)



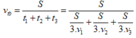

\(20ph=\dfrac{1}{3}h,35ph=\dfrac{7}{12}h\)
Vận tốc trung bình trên đoạn đường đầu:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{12}{\dfrac{1}{3}}=36\left(\dfrac{km}{h}\right)\)
Vận tốc trung bình trên đoạn đường sau:
\(v_2=\dfrac{S_2}{t_2}=\dfrac{24}{\dfrac{7}{12}}=\dfrac{288}{7}\left(\dfrac{km}{h}\right)\)
Vận tốc trung bình trên cả 2 quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{12+24}{\dfrac{1}{3}+\dfrac{7}{12}}=\dfrac{432}{11}\left(\dfrac{km}{h}\right)\)