Gọi x1, x2 là nghiệm của phương trình |46x + 49| = |19x + 17|. Tìm |x1 − x2|.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
31 tháng 12 2021
Answer:
\(\left|46x+49\right|=\left|19x+17\right|\)
\(\Rightarrow\orbr{\begin{cases}46x+49=19x+17\\46x+49=-19x-17\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-32}{27}\\x=\frac{-66}{65}\end{cases}}\)
\(\Rightarrow\left|x_1-x_2\right|=\left|\frac{-32}{27}-\left(\frac{-66}{65}\right)\right|=\frac{298}{1755}\)
CM
30 tháng 4 2019
Phương trình ⇔ 4 x − 17 ≥ 0 x 2 − 4 x − 5 = 4 x − 17 2
⇔ x ≥ 17 4 x 2 − 5 x − 5 2 = 4 x − 17 2
⇔ x ≥ 17 4 ( x 2 − 8 x + 12 ) ( x 2 − 22 ) = 0 ⇔ x ≥ 17 4 x 2 − 8 x + 12 = 0 x 2 − 22 = 0
⇔ x ≥ 17 4 x = 2 ∨ x = 6 x = ± 22 ⇔ x = 6 x = 22 ⇒ P = 22 2 + 6 = 28
Đáp án cần chọn là: C
7 tháng 4 2022
a.\(\Delta=\left(-4\right)^2-4.2m=16-8m\)
Để pt có nghiệm x1, x2 thì \(\Delta>0\)
\(\Leftrightarrow16-8m>0\)
\(\Leftrightarrow-8m>-16\)
\(\Leftrightarrow m< 2\)
b.
Theo hệ thức Vi-ét, ta có:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=2m\end{matrix}\right.\)
\(x_1^2+x_2^2-x_1-x_2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2-\left(x_1+x_2\right)=16\)
\(\Leftrightarrow4^2-2.2m-4-16=0\)
\(\Leftrightarrow-4m-4=0\)
\(\Leftrightarrow m=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 4 2022
a.
Phương trình có 2 nghiệm khi:
\(\Delta'=4-2m\ge0\Rightarrow m\le2\)
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=2m\end{matrix}\right.\)
\(x_1^2+x_2^2-x_1-x_2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=16\)
\(\Leftrightarrow16-4m-4=16\)
\(\Leftrightarrow m=-1\) (thỏa mãn)
CL
cho x1, x2, x3 là 3 nghiệm của phương trình x^3-19x-30=0. Giá trị của Bt B= x1^2 + x2^2 + x3^2 là...
2
12 tháng 8 2021
x3 - 19x - 30 = 0
<=> x3 - 5x2 + 5x2 - 25x + 6x - 30 = 0
<=> x2( x - 5 ) + 5x( x - 5 ) + 6( x - 5 ) = 0
<=> ( x - 5 )( x2 + 5x + 6 ) = 0
<=> ( x - 5 )( x2 + 3x + 2x + 6 ) = 0
<=> ( x - 5 )[ x( x + 3 ) + 2( x + 3 ) ] = 0
<=> ( x - 5 )( x + 3 )( x + 2 ) = 0
đến đây dễ rồi :)
AD
12 tháng 8 2021
\(x^3-19x-30=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-5=0\\x+2=0\\x+3=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\x=-2\\x=-3\end{cases}}}\)
Vậy B=x12+x22+x32
B=52+(-2)2+(-3)2
B=25+4+9
B=38
#H
NV
1
CM
11 tháng 9 2017
Phương trình x 2 − 20x − 17 = 0 có = 468 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 20 x 1 . x 2 = − 17
Ta có
C = x 1 3 + x 2 3 = x 1 3 + 3 x 1 2 x 2 + 3 x 1 x 2 2 + x 2 3 − 3 x 1 2 x 2 − 3 x 1 x 2 2 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 ) = 2 3 – 3 . ( − 17 ) . 20 = 9020
Đáp án: D
7 tháng 5 2021
a) Đây là phương trình bậc 2 ẩn x có
Δ = (-m)2 - 4(m-1)
= m2-4m+4 = (m-2)2
Do (m-2)2≥0 ∀m => Δ≥0 ∀m
Vậy phương trình luôn có nghiệm với mọi m.
b) Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)
\(x_1=2x_2\left(3\right)\)
Từ (1)(3) ta có hệ phương trình: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1=2x_2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}3x_2=m\\x_1=2x_2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x_2=\dfrac{m}{3}\\x_1=\dfrac{2m}{3}\end{matrix}\right.\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
<=> 2m2 = 9(m - 1)
<=> 2m2 - 9m + 9 = 0
<=> (m - 3)(2m - 3) = 0
<=> \(\left[{}\begin{matrix}m-3=0\\2m-3=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy tại m ∈\(\left\{3;\dfrac{3}{2}\right\}\) thì hai nghiệm của phương trình thoả mãn x1=2x2
KV
7 tháng 5 2021
a) Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.1.\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2\ge0\) với mọi m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Do phương trình luôn có nghiệm với mọi m
Theo định lý Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-m\right)}{1}=m\left(1\right)\\x_1x_2=\dfrac{c}{a}=\dfrac{m-1}{1}=m-1\left(2\right)\end{matrix}\right.\)
Mà \(x_1=2x_2\), thay vào (1) ta có:
\(2x_2+x_2=3\Leftrightarrow3x_2=m\Leftrightarrow x_2=\dfrac{m}{3}\)
\(\Rightarrow x_1=2x_2=\dfrac{2m}{3}\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
\(\Leftrightarrow2m^2=9m-9\)
\(\Leftrightarrow2m^2-9m+9=0\) (*)
\(\Delta_m=\left(-9\right)^2-4.2.9=9\)
Phương trình (*) có 2 nghiệm:
\(m_1=\dfrac{-\left(-9\right)+\sqrt{9}}{2.2}=3\)
\(m_2=\dfrac{-\left(-9\right)-\sqrt{9}}{2.2}=\dfrac{3}{2}\)
Vậy \(m=3;m=\dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm \(x_1;x_2\) thỏa mãn \(x_1=2x_2\)
8 tháng 3 2022
a: Thay x=-3 vào pt, ta được:
9+6m+2m+1=0
=>8m+10=0
hay m=-5/4
b: \(\text{Δ}=\left(-2m\right)^2-4\left(2m+1\right)\)
\(=4m^2-8m-4\)
\(=4\left(m-2\right)\left(m+1\right)\)
Để phương trình có hai nghiệm thì (m-2)(m+1)>=0
=>m>=2 hoặc m<=-1
c: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2+2x_1x_2=16\)
\(\Leftrightarrow\left(2m\right)^2=16\)
=>2m=4 hoặc 2m=-4
=>m=2(nhận) hoặc m=-2(nhận)
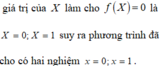
\(\left|46x+49\right|=\left|19x+17\right|\)
\(\Rightarrow\orbr{\begin{cases}46x+49=19x+17\\46x+49=-19x-17\end{cases}\Rightarrow\orbr{\begin{cases}x=-\frac{32}{27}\\x=-\frac{66}{65}\end{cases}}}\)
\(\Rightarrow\left|x_1-x_2\right|=\left|-\frac{32}{27}-\frac{66}{65}\right|=....\)