Cho hình chóp S.ABCD có đáy ABCD là hbh tâm O. Gọi M là trung điểm BC. P thuộc SA sao cho AP=2SP
a, Tìm giao điểm của PM và (SBD). Chứng minh SC//(MDP)
b, (Q) đi qua P và song song với AD, SB. Tìm thiết diện của chóp cắt bởi (Q)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
Gọi (P) là mặt phẳng qua M, song song DE và SC
Gọi O là giao điểm AC, BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM||SC\Rightarrow O\in\left(P\right)\)
Trong mp (SBD), gọi F là trung điểm BE \(\Rightarrow OF\) là đường trung bình tam giác BDE
\(\Rightarrow OF||DE\Rightarrow F\in\left(P\right)\)
Trong mp (SBC), qua F kẻ đường thẳng song song SC cắt BC tại G
\(\Rightarrow G\in\left(P\right)\)
Trong mp (ABCD), nối GO kéo dài cắt AD tại H
\(\Rightarrow H\in\left(P\right)\)
\(\Rightarrow\) Thiết diện của (P) và chóp là tứ giác MFGH (và tứ giác này không có điều gì đặc biệt)
CM
1 tháng 7 2018
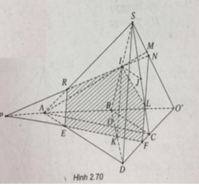
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
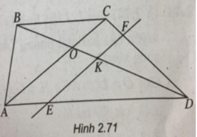
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do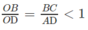 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.
