Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Lấy chiều dương là chiều chuyển động thì quãng đường và vận tốc của vật sau 10s đầu là:
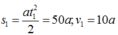
Trong 10s sau vật chuyển động với vận tốc đầu
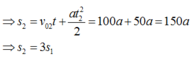
Chú ý: Khi một vật bắt đầu chuyển động thẳng biến đổi đều từ trạng thái nghỉ thì chuyển động đó phải là chuyển động thẳng nhanh dần đều
Gia tốc của vật:
\(s=\dfrac{1}{2}at^2\Leftrightarrow50=\dfrac{1}{2}a\cdot10^2\Rightarrow a=1\left(m/s^2\right)\)
Quãng đường vật đi được trong 6s đầu:
\(S_6=\dfrac{1}{2}a\cdot t'^2=\dfrac{1}{2}\cdot1\cdot6^2=18\left(m\right)\)
Quãng đường vật đi được trong 4s cuối:
\(S_4=S-S_6=50-18=32\left(m\right)\)
+ Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
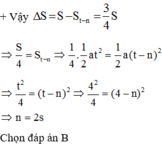
Gọi t là thời gian đi cả quãng đường.
\(t_1\) là thời gian đi \(\dfrac{1}{4}\) đoạn đường đầu.
Ta có: \(S=\dfrac{1}{2}at^2\)
\(\dfrac{1}{4}S=\dfrac{1}{2}at^2_1\)
\(\Rightarrow\dfrac{S}{\dfrac{1}{4}S}=\dfrac{\dfrac{1}{2}at^2}{\dfrac{1}{2}at^2_1}=\dfrac{t^2}{t^2_1}\)\(\Rightarrow t_1=\dfrac{t}{2}\)
Thời gian vật đi \(\dfrac{3}{4}\) đoạn đường cuối:
\(t'=t-t_1=t-\dfrac{t}{2}=\dfrac{t}{2}\left(h\right)\)
Giải: Ta có v 0 = 0 ( m / s )
Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
Vậy Δ S = S − S t − n = 3 4 S ⇒ S 4 = S t − n ⇒ 1 4 . 1 2 a t 2 = 1 2 a ( t − n ) 2 ⇒ t 2 4 = ( t − n ) 2 ⇒ 4 2 4 = ( 4 − n ) 2 ⇒ n = 2 s
Gia tốc vật: \(S=\dfrac{1}{2}at^2\)
\(\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot50}{10^2}=1\)m/s2
Quãng đường vật đi trong 4s cuối tức vật đã đi đc 6s:
\(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot1\cdot6^2=18m\)
Chọn C
D