Bài 1: Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho DB/DC = 1/2. Đường thẳng qua D song song với AB cắt AC tại E; Đường thẳng qua D song song AC cắt AB tại Fa) So sánh các tỉ số AF/AB; AE/AC.
b) Gọi M là trung điểm của AC. CMR: EF// BM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2017
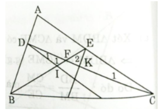
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
Tương tự ta có: ΔDFB ∼ ΔKFE
Từ (1), (2) ⇒ FC.FI = FB.FK
Do đó theo định lí Talét đảo ta có KI // BC.
Dễ thôi:vvv
a) Vì DF//AC
=> \(\dfrac{AF}{AB}=\dfrac{CD}{BC}=\dfrac{2}{1+2}=\dfrac{2}{3}\)
Vì DE//AB
=> \(\dfrac{AE}{AC}=\dfrac{BD}{BC}=\dfrac{1}{1+2}=\dfrac{1}{3}\)
b) Ta có: \(\dfrac{AE}{AC}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{2AM}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{AM}=\dfrac{2}{3}\)
Lại có: \(\dfrac{AF}{AB}=\dfrac{2}{3}\)
=> \(\dfrac{AF}{AB}=\dfrac{AE}{AM}\)
=> EF//BM(theo đ/lý Ta-lét đảo)