Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng BC + AH > AB + AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
5 tháng 4 2021
a) Xét tam giác ABC và tam giác HAC có:
BAC = AHC =90
ABC = HAC (cùng phụ với HAB)
=> ABC đồng dạng HAC (g.g)
b) Vì ABC đồng dạng HAC
=> AB/BC = AH/AC
=> AB.AC=BC.AH
c) Vì AB.AC = BC.AH
=> AB^2.AC^2= BC^2 . AH^2
Mà BC^2=AB^2+AC^2 (định lý pytago ở tam giác ABC vuông tại A)
=> AB^2.AC^2= (AB^2+AC)^2.AH^2
=> 1/AH^2 =1/AB^2 +1/AC^2
FC
1
TA
25 tháng 3 2017
Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).
ND
1
DT
0
6 tháng 3 2021
a) Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) là góc chung
Do đó: ΔABH\(\sim\)ΔCBA(g-g)
CM
15 tháng 10 2018
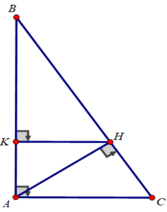
c) Xét tam giác ABC vuông tại A có ∠B = 30 0 , AC = 6 cm:
AB = AC.cotgB = 6.cotg 30 0 = 2 3 (cm)
AC = BC.sinB ⇒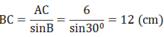 
Tam giác ABC vuông tại A có AH là đường cao nên
AH.BC = AB.AC ⇒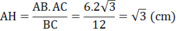 
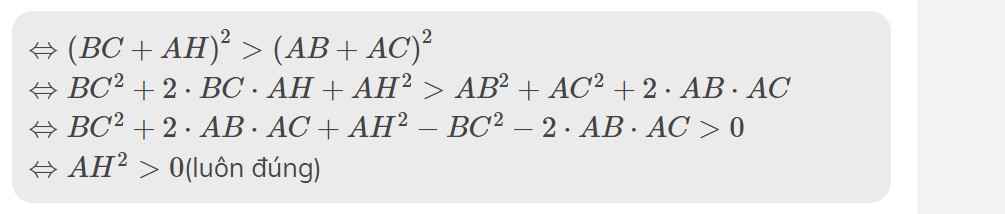
\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)