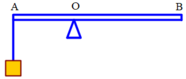
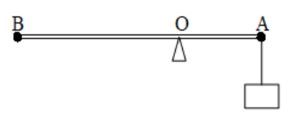
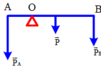
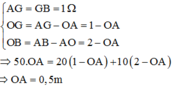có một thanh sắt AB để trên một điểm tựa O theo nguyên lý đòn bẩy, cả hai khoảng cách AB đều cân bằng nhau. Người ta treo một vật có trọng lượng 120N ở đầu A, khoảng cách từ A đến điểm O bằng 1/3 khoảng cách từ O đến B. hỏi phải treo ở đầu B một vật có trọng lượng bao nhiêu để đòn bẩy cân bằng(bỏ khối lượng của thanh sắt AB)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


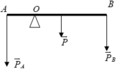
Ta có:
P = m g = 2.10 = 20 ( N ) ; P A = m A . g = 5.10 = 50 ( N ) ; P B = m B . g = 1.10 = 10 ( N )
Theo điều kiện cân bằng Momen lực: MA = MP + MB
⇒ P A . O A = P . O G + P B . O B
AG = GB = 1m
OG = AG – OA = 1 – OA
OB = AB – AO = 2 – OA
=> 50. OA = 20 (1- OA) + 10( 2 – OA )
=> OA = 0,5m

Bài 1.
a)\(OA=40cm\Rightarrow OB=160-40=120cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1\cdot l_1=F_2\cdot l_2\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{l_2}{l_1}=\dfrac{OB}{OA}=\dfrac{120}{40}=3\)
\(\Rightarrow F_2=\dfrac{F_1}{3}=\dfrac{P_1}{3}=\dfrac{10m_1}{3}=\dfrac{10\cdot9}{3}=30N\)
\(\Rightarrow m_2=\dfrac{P_2}{10}=\dfrac{F_2}{10}=\dfrac{30}{10}=3kg\)
b)Vật \(m_2\) giữ nguyên không đổi. \(\Rightarrow F_2=P_2=30N\)
\(OB'=60cm\Rightarrow OA'=160-60=100cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1'\cdot l_1'=F_2\cdot l_2'\)
\(\Rightarrow F_1'=\dfrac{F_2\cdot l_2'}{l_1'}=\dfrac{30\cdot60}{100}=18N\) \(\Rightarrow m_1'=1,8kg\)
Mà \(m_1=9kg\)
\(\Rightarrow\) Phải giảm vật đi một lượng là:
\(\Delta m=m_1-m_1'=9-1,8=7,2kg\)
Bài 2.
a)Áp dụng hệ cân bằng của đòn bẩy:
\(\dfrac{F_1}{F_2}=\dfrac{OA}{OB}=\dfrac{10m_1}{10m_2}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\Rightarrow2OA=3OB\left(1\right)\)
Mà \(OA+OB=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=72cm\\OB=48cm\end{matrix}\right.\)
Vậy O nằm cách A và B lần lượt một đoạn là 72cm và 48cm.
b)Giữ nguyên vật 2 \(\Rightarrow F_2=P_2=10m_2=40N\)
Tăng khối lượng \(m_1\) lên 2kg thì \(F_1=P_1=10\cdot\left(2+6\right)=80N\)
Để thanh AB nằm cân bằng:
\(F_1\cdot OA'=F_2\cdot OB'\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{OB'}{OA'}=\dfrac{80}{40}=2\)
\(\Rightarrow OB'=2OA'\left(1\right)\)
Mà \(OA'+OB'=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA'=40cm\\OB'=80cm\end{matrix}\right.\)
Vậy O nằm trên AB cách A và B lần lượt là 40cm và 80 cm.

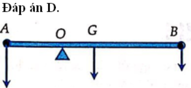
Dễ thấy, nếu O nằm giữa G và B thì thanh không thể cân bằng nên O nằm giữa A và G. Quy tắc mômen lực đối với trục qua O:
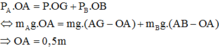

Tóm tắt :
a/ AB = 160 cm A O B
m1 = 9 kg ( P= F1 = 10m = 90N
OA = 40 cm
m2 =? m1 = 9kg
b/ OB = 60 cm
m1 =? Thêm hay bớt bao nhiêu?
Giải :
a/ Theo bài ra ta có:
OA = 40 cm
( OB = AB – OA = 160 – 40 = 120 cm
Aùp dụng hệ thức cân bằng của đòn bẩy : =
( Lực tác dụng lên đầu B là : F2 = = 30 N
Mà F2 = 10.m2 ( m2 kg
Vậy để thanh AB cân bằng, ta phải treo ở đầu B một vật m2 = 3kg.
b/ Ta có : OB = 60 cm
( OA = AB – OB = 160 – 60 = 100 cm
Aùp dụng hệ thức cân bằng của đòn bẩy: =
Để thanh AB cân bằng thì phải tác dụng vào đầu A một lực:
F’1 = = = 18N
Mà F1’ = 10.m1’ ( m1’ = 1,8 kg
Khi đó chỉ cần treo vào đầu A một vật có khối lượng là 1,8kg
Vậy phải bớt vật m1 đi một lượng là :
9 kg – 1,8 kg = 7,2 kg
a/ Ta có: OA = 40cm
\(\Rightarrow OB=AB-OA=160-40=120\) cm
Trọng lượng của vật m1:
P1 = F1 = 10.m1 = 90N
Áp dụng hệ thức cân bằng của đòn bảy:
\(\frac{F_1}{F_2}=\frac{l_2}{l_1}=\frac{OB}{OA}\)
Lực tác dụng vào đầu B:
\(F_2=\frac{F_1.OA}{OB}=30N\)
Vậy để thanh AB cân bằng thì phải treo vào đầu B vật m2 = 3Kg.
b/ Ta có: OB = 60cm
\(OA=AB-OB=160-60=100\) cm
Áp dụng hệ thức cân bằng của đòn bảy, để thanh AB cân bằng thì lực tác dụng vào đầu A:
\(F'=\frac{F_2l_2}{l_1}=\frac{F_2.OB}{OA}=\frac{30.60}{100}=18\) N
Vậy vật m1 = 1,8Kg tức là vật m1 phải bớt đi 7,2Kg.

gọi l1 là chiều dài cánh tay đòn 1 ( ở đây là OA) l2 là chiều dài cánh tay đòn 2 ( ở đây là OB)
l1+l2=150 cm =1,5 m (1)
m1=3kg => P1=30(N)
m2=6kg => P2=60(N)
Để hệ thống cân bằng thì:
m1.l1=m2.l2
=> 30l1=60l2 => l1 - 2l2= 0 ( đơn giản mỗi vế cho 30) (2)
Từ (1) và (2) ta có hệ phương trình
l1+l2=1,5
l1 - 2l2=0
=> l1=1 (m)
l2=0,5(m)

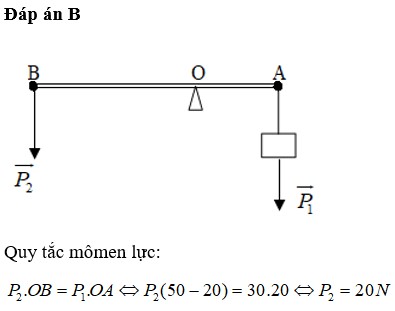
Đáp án B
Áp dụng quy tắc momen lực: MA = MP + MB
↔ P1. OA = P. OI + P2. OB
AI = IB = 1m
OI = AI – OA = 1 – OA
OB = OI – IB = 2 – OA
↔ 50. OA = 20 (1- OA) + 10(2 – OA) → OA = 0,5m.