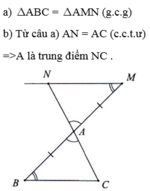
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Qua M kẻ đường thẳng a song song với BC, đường thẳng a cắt tia CA tại N. Chứng minh: a) ABC = AMN. b) A là trung điểm của NC. c) Nối B với N, C với M, hãy đặt thêm câu hỏi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
25 tháng 8 2020
\(\left(1-a+a^2\right)\left(1-b+b^2\right)=1-b+b^2-a+ab-ab^2+a^2-a^2b+a^2b^2.\)
\(=\frac{2-2a-2b+2b^2+2ab+2a^2-2ab\left(a+b\right)+2a^2b^2}{2}\)\(=\frac{\left(a-b\right)^2+1+a^2b^2+\left(1-a\right)^2\left(1-b\right)^2}{2}\ge\frac{1+a^2b^2}{2}\)
Tương Tự : \(\left(1-c+c^2\right)\left(1-d+d^2\right)\ge\frac{1+c^2d^2}{2}\)
26 tháng 8 2020
(1-a+a2) (1-b+b2) = 1-b+b2-a+ab-ab2+a2-a2b+a2b2.
=2-2a-2b+2b2+2ab+2a2-2ab(a+b)+2a2b2 =(a-b)2+1+a2b2+(1-a)2(1-b)2> 1+a2b2 2 2 Tương Tự:(1-c+c2) (1-d+d2) > 1+c2d2 2
19 tháng 3 2020
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
19 tháng 3 2020
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
YP
14 tháng 4 2022
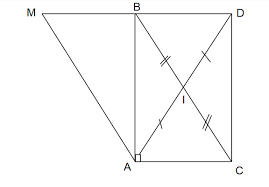
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đối đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
YP
14 tháng 4 2022
Bạn ơi, vì mình k thể kí hiệu góc. Nên bạn tự ghi góc vào bài làm của mình nhé
4 tháng 11 2018
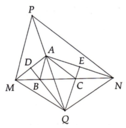
A)
xét tam giác ABC và tam giác ADC
có : góc ADC = góc ABC
AB=AD ( tia đối )
AC chung
=> tam giác ABC = tam giác ADC (c-g-c)
=> góc ACB = góc ACD
=> AC LÀ phân giác góc BCD
b)
ý 2 câu b : cm DC//AE
có tam giác ABC vuông tại A
mà AM là đường trung tuyến
=> AM=MC
=> tam giác AMC cân tại M
=> góc MAC = góc MCA ( tam giác cân )
mà góc MCA = góc ACD ( phân giác )
=> MAC = góc ACD
mà 2 góc này vị trí so le trong
=> DC//AE
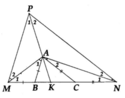
a: Xét ΔABC và ΔAMN có
AB=AM
\(\widehat{BAC}=\widehat{MAN}\)
AC=AN
Do đó: ΔABC=ΔAMN