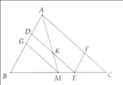
cho tam giác ABC trung tuyến AM, CN cắt nhau tại G. K là điểm nằm trên BC , đường thẳng qua K song song với CN cắt AB ở D, đường thằng qua K song song với BM cắt AC ở E. Gọi I là giao điểm của KG với DE. Chứng minh: I là trung điểm của DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2023
Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>K là trung điểm của BC
Xét ΔBNC co
K là trung điểm của BC
KD//NC
=>D là trung điểm của NB
Xét ΔBMC có
K làtrung điểm của CB
KE//BM
=>E là trung điểm của MC
BD=1/2BN=1/4AB
=>AD=3/4AB
CE=1/2CM=1/4AB
=>AE=3/4AC
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét ΔABK có DI//BK
nên DI/BK=AI/AK
Xét ΔACK có IE//KC
nên IE/KC=AI/AK
=>DI/BK=IE/KC
=>DI=IE
=>I là trung điểm của DE
K
30 tháng 3 2020
Qua K vẽ đường thẳng // với AB cắt AC tại H.
=> AHKD là hình bình hành => DK = AH (1)
Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH
Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1
=> DH // BC (định lí chùm đường thẳng đồng quy đảo)
Xét ∆ ADH và ∆ FEC có:
AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)
=> AH = CF (2)
Từ (1) và (2) => CF = DK (đpcm)
GL
31 tháng 3 2020
Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)
Dựng MG//AC và MM là trung điểm cạnh BC
⇒GM là đường trung bình ΔABC
=⇒G là trung điểm cạnh AB ⇒AG=BG
Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)
=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)
Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF
=> CF=DK (đpcm)
Nguồn: thuynga
