Cô giáo vẽ lên bảng hình tứ giác ABCD. Sau đó cô lấy thêm một điểm E nằm ngoài tứ giác ABCD. Biết khi nối 5 điểm A,B,C,D lại với nhau,ta được 3 hình tứ giác nhận 4 trong 5 điểm A:B:C:D:E làm đỉnh .Hỏi trong hình vẽ đó có tất cả bao nhiêu hình tam giác nhận 3 trong 5 điểm A:B:C:D:E làm đỉnh?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 7 2015
Nếu trong 5 điểm A; B; C; D; E không có 3 điểm nào thẳng hàng => 4 điểm bất kì trong 5 điểm đều tạo thành tứ giác => Các tứ giác tạo thành là: ABCD; ABCE; ACDE; ABDE; BCDE; nhiều hơn 3 tứ giác
=> Điểm E thẳng hàng với hai điểm bất kì trong 4 điểm AB; B; C; D
Coi A; B ; E thẳng hàng:
Mỗi đỉnh A; B ; E nối với C; D được 1 tam giác => có 3 tam giác
Mỗi đỉnh D; C nối với A; B ta được 1 tam giác => có 2 tam giác
Mỗi đỉnh D; C nối với A; E ta được 1 tam giác => có 2 tam giác
Mỗi đỉnh D; C nối với E; B ta được 1 tam giác => có 2 tam giác
vậy có tất cả là : 3 + 2 + 2 + 2 = 9 tam giác
9 tháng 7 2015
Khi nối 5 điểm A; B; C ; D; E lại với nhau, ta được 3 hình tứ giác nhận 4 trong 5 điểm A; B; C ; D; E làm đỉnh. Nên điểm E thẳng hàng với 2 trong 4 điểm của tứ giác ABCD. Hình vẽ:
Trong hình vẽ đó có tất cả 9 hình tam giác nhận 3 trong 5 điểm A ; B; C; D; E làm đỉnh.
CM
11 tháng 9 2018
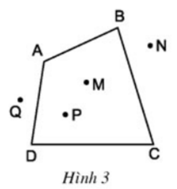
a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A
Hai đỉnh đối nhau: A và C, B và D
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD
c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB
Hai cạnh đối nhau: AB và CD, AD và BC
d) Góc: ∠A , ∠B , ∠C , ∠D
Hai góc đối nhau: ∠A và ∠C , ∠B và ∠D
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q
6 tháng 1 2017
Ta có:
*S ABCD = S ABC + S ACD
Hay
S ABCD = S 1 + S 2 + S 3 + S 4 + S 5 + S 6 + S 7 + S 8
*Vì MB = MC nên:
S1 + S2 = S ABC : 2 ( Tam giác ABM và ABC có chung đường cao hạ từ A và BM = BC : 2 )
*Tương tự: S 7 + S 8 = S ACD : 2 ( Tam giác CED và ACD có chung đường cao hạ từ C và DE = AD : 2 )
*Do đó:
S 1 + S 2 + S 7 + S 8 = S 3 + S 4 + S 5 + S 6 = S ABCD : 2
*Lại có:
S 2 + S 3 = S 5 + S 6 (Hai tam giác BME và CME có chung đường cao hạ từ E và BM = CM)
S 5 + S 8 = S 3 + S 4 (Hai tam giác AME và DME có chung đường cao hạ từ M và ED = EA)
==>S 2 + S 8 = S 4 + S 6
*Vì S 1 + S 7 + (S 2 + S 8) = S 3 + S 5 + (S 4 + S 6) mà S 2 + S 8 = S 4 + S 6
Nên S 1 + S 7 = S 3 + S 5
==>S 3 + S 5 = 3 cm2 + 5 cm2 = 8 cm2
Hay SEHKMN = 8 cm2
Đáp số : 8 cm2
