một đa giác có số đường chéo nhìu hơn số cạnh là 12 tìm số cạnh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
BS
0
LM
1
16 tháng 1 2021
Ta có cách tính cạnh của một đa giác là :
\(\dfrac{\left(a-3\right).a}{2}\),trong đó a là số đỉnh \(\Rightarrow\) đa giác có a cạnh
\(\Rightarrow\dfrac{\left(a-3\right).a}{2}-a=7\Leftrightarrow\dfrac{a^2-3a-2a}{2}=7\\ \Rightarrow a^2-5a=14\)
\(\Rightarrow a\left(a-5\right)=14.\)
Vì a là số cạnh nên a>1 và a>a-5
\(\Rightarrow a\left(a-5\right)=2.7\Rightarrow\)\(\left\{{}\begin{matrix}a=7\\\\a-5=2\end{matrix}\right.\)\(\Rightarrow a=7\)
Vậy đa giác có 7 cạnh
PT
5
YN
16 tháng 12 2021
Answer:
Số đường chéo của đa giác \(n\left(n-3\right):2\)
Có:
\(n\left(n-3\right):2=n+42\)
\(n\left(n-3\right)=2n+84\)
\(n^2-5n=84\)
\(n^2-2.2,5+\left(2,5\right)^2=84+\left(2,5\right)^2\)
\(\left(n-2,5\right)^2=90,25\)
\(\Rightarrow n-2,5=9,5\left(n>0\right)\)
\(\Rightarrow n=12\)
Vậy đa giác có tổng cộng là 12 cạnh
DX
16 tháng 12 2021
anh ơi anh giúp em bài TA đi rồi e giúp anh cho , e biết làm
CM
15 tháng 11 2019
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 
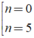
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A
IM
13 tháng 9 2016
Gọi số cạnh của đa giác là 10 + k( \(k\in\)N* )
\(\Rightarrow\frac{\left(10+k\right)\left(10+k+3\right)}{2}< 60\)
\(\Rightarrow\frac{\left(10+k\right)\left(13+k\right)}{2}< 60\)
\(\Rightarrow\frac{130+10k+13k+k^2}{2}< 60\)
\(\Rightarrow\frac{130+23k+k^2}{2}< 60\)
\(\Rightarrow130+23k+k^2< 120\)
\(\Rightarrow k^2+2.k.\frac{23}{2}+\frac{23^2}{2^2}+\frac{1551}{16}< 120\)
\(\Rightarrow\left(k+11,5\right)^2< \frac{369}{16}< \frac{400}{16}\)
\(\Rightarrow\left(k+11,5\right)^2< 5^2\) (1)
Mà \(k\in\)N*
=> k+11 , 5 > 11,5 > 5
\(\Rightarrow\left(k+11,5\right)^2>5^2\) (2)
So sánh (1) và (2)
=> Mâu thuẫn .
Vậy không có đa giác cần tìm .
