Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC vuông tại A với AB > AC, gọi AH là đường cao kẻ từ A thì ta có:
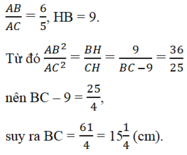

Gọi x là độ dài cạnh góc vuông nhỏ
Độ dài cạnh góc vuông lớn là: x+1
Theo đề, ta có phương trình:
\(x^2+\left(x+1\right)^2=25\)
\(\Leftrightarrow2x^2+2x+1-25=0\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\left(loại\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
Chu vi tam giác vuông đó là:
\(3+4+5=12\left(m\right)\)
Gọi cạnh góc vuông nhỏ hơn của tam giác vuông đó là a(m)(a>0)
Theo đề ra, ta có:
\(a^2+\left(a+1\right)^2=25\\ \Rightarrow a^2+a^2+2a+1=25\\ \Rightarrow2a^2+2a=24\\ \Rightarrow a\left(a+1\right)=12=3.4\\ \Rightarrow a=3\)
Chu vi tam giác đó là:
3 + 3 + 1 + 5 = 12(m)

câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5

a/ Kẻ đường cao AH => BH là hình chiếu của AB trên BC và CH là hình chiếu của AC trên BC
Giả sử \(\frac{AB}{AC}=k\Rightarrow\frac{AB^2}{AC^2}=k^2\)
Ta có \(AB^2=BH.BC;AC^2=CH.BC\Rightarrow\frac{AB^2}{AC^2}=\frac{BH}{CH}=k^2\)
b/ Áp dụng câu A sẽ tính được tỷ số hình chiếu 2 cạnh góc vuông trên BC là mà biết chiều dài BC=82 bài toán là dạng tìm 2 số khi biết tổng và tỷ ở lớp 5 rồi bạn tự giải nốt nhé

Gọi 2 tam giác đó lần lượt là `\DeltaABC,\DeltaA'B'C'`
Cạnh góc vuông là cạnh huyền của 2 tam giác lần lượt là `AB,BC` và `A'B',B'C`
Xét tam giác `\DeltaABC` và `\DeltaA'B'C'`:
`(AB)/(BC)=(A'B')/(B'C')`
`\hat{BAC}=\hat{B'A'C'}=90^o`
`=>\DeltaABC~\DeltaA'B'C'`
Mong mọi người giúp đỡ.